Article contents
Spirals of Riemann’s Zeta-Function — Curvature, Denseness and Universality
Published online by Cambridge University Press: 05 October 2023
Abstract
This paper deals with applications of Voronin’s universality theorem for the Riemann zeta-function 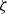 $\zeta$. Among other results we prove that every plane smooth curve appears up to a small error in the curve generated by the values
$\zeta$. Among other results we prove that every plane smooth curve appears up to a small error in the curve generated by the values 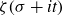 $\zeta(\sigma+it)$ for real t where
$\zeta(\sigma+it)$ for real t where 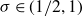 $\sigma\in(1/2,1)$ is fixed. In this sense, the values of the zeta-function on any such vertical line provides an atlas for plane curves. In the same framework, we study the curvature of curves generated from
$\sigma\in(1/2,1)$ is fixed. In this sense, the values of the zeta-function on any such vertical line provides an atlas for plane curves. In the same framework, we study the curvature of curves generated from 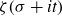 $\zeta(\sigma+it)$ when
$\zeta(\sigma+it)$ when 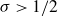 $\sigma>1/2$ and we show that there is a connection with the zeros of
$\sigma>1/2$ and we show that there is a connection with the zeros of 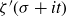 $\zeta'(\sigma+it)$. Moreover, we clarify under which conditions the real and the imaginary part of the zeta-function are jointly universal.
$\zeta'(\sigma+it)$. Moreover, we clarify under which conditions the real and the imaginary part of the zeta-function are jointly universal.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 176 , Issue 2 , March 2024 , pp. 325 - 338
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
Footnotes
Supported by the Austrian Science Fund (FWF) project number M 3246-N.
References
- 1
- Cited by


