Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T00:59:27.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral rigidity and discreteness of 2233-groups

Published online by Cambridge University Press:  01 January 2008

PETER BUSER ,
NICOLE FLACH ,
KLAUS-DIETER SEMMLER ,
COLIN MACLACHLAN  and
GERHARD ROSENBERGER
PETER BUSER
Affiliation:
Section de Mathématiques, École Polytechnique Fédérale de Lausanne, Station 8, CH-1015 Lausanne, Switzerland. e-mail: [email protected], [email protected], [email protected]
NICOLE FLACH
Affiliation:
Section de Mathématiques, École Polytechnique Fédérale de Lausanne, Station 8, CH-1015 Lausanne, Switzerland. e-mail: [email protected], [email protected], [email protected]
KLAUS-DIETER SEMMLER
Affiliation:
Section de Mathématiques, École Polytechnique Fédérale de Lausanne, Station 8, CH-1015 Lausanne, Switzerland. e-mail: [email protected], [email protected], [email protected]
COLIN MACLACHLAN
Affiliation:
Department of Mathematical Sciences, University of Aberdeen, Aberdeen AB24 3UE, Scotland. e-mail: [email protected]
GERHARD ROSENBERGER
Affiliation:
Fachbereich Mathematik, Lehrstuhl LSVI, Universität Dortmund, Vogelpothsweg 87, D-44227 Dortmund, Germany. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we describe methods for dealing with the trace spectrum of a subgroup of PSL(2, 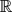) generated by four elliptic elements α, β, γ, δ of respective orders 2, 2, 3, 3, satisfying αβγδ = 1. We give a parametrization and a fundamental domain in the parameter space of such groups. Furthermore we construct an algorithm that decides whether or not a given group is discrete and which moves the discrete groups into the fundamental domain. Our main result is that any two discrete such groups are isospectral if and only if they are conjugate in (2, ).

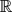In the Appendix we consider pairs of subgroups of (2, 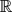) that arise from non-conjugate maximal orders in a quaternion algebra over a number field. We show that for the isospectrality of such pairs there is a peculiar exception in the case where the groups contain elements of both orders 2 and 3.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 1 , January 2008 , pp. 145 - 180
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beardon, A. F.. The geometry of discrete groups. Graduate Texts in Mathematics, vol. 91. (Springer-Verlag, 1995).Google Scholar
[2]Binotto, A.. Surfaces de Riemann de type (0,3) et (1,1): Polyn omes au service de letude spectrale. Ph.D.thesis, \'Ecole Polytechnique Federale de Lausanne (2000).Google Scholar
[3]Brooks, R.. Constructing isospectral manifolds. Amer. Math. Monthly 95 (1988), 823–839.Google Scholar
[4]Brooks, R., Gornet, R. and Gustafson, W. H.. Mutually isospectral Riemann surfaces. Adv. Math. 138 (1998), 306–322.Google Scholar
[5]Brooks, R. and Tse, R.. sospectral surfaces of small genus. Nagoya Math. J. 107 (1987), 13–24.Google Scholar
[6]Buser, P.. Isospectral Riemann surfaces. Ann. Inst. Fourier (Grenoble) 36 (1986), 167–192.Google Scholar
[7]Buser, P.. Geometry and spectra of compact Riemann surfaces. Progr. Math. 106 (Birkhäuser, 1992).Google Scholar
[8]Buser, P. and Semmler, K.-D.. The geometry and spectrum of the one holed torus. Comment. Math. Helv. 63 (1988), 259–274.CrossRefGoogle Scholar
[9]Chinburg, T. and Friedman, E.. An embedding theorem for quaternion algebras. J. London Math. Soc. 60 (1999), 33–44.CrossRefGoogle Scholar
[10]Cohen, H.. PARI-GP: A software package for computer-aided number theory. Available at http://www.parigp-home.de/ (2001)Google Scholar
[11]Rham, G. de. Sur les polygones générateurs de groupes fuchsiens. Enseignement Math. 17 (1971), 49–61.Google Scholar
[12]Dianu, R.. Sur le spectre des tores pointés. Ph.D.thesis, École Polytechnique Fédérale de Lausanne (2000).Google Scholar
[13]Fine, B. and Rosenberger, G.. Classification of all generating pairs of two generator Fuchsian groups. Groups '93, Galway/St Andrews. London Math. Soc. Lecture Notes, vol. 211 (1995), 205–232.Google Scholar
[14]Fine, B., Rosenberger, G. and Stille, M.. Nielsen transformations and applications: a survey. Groups–-Korea '94 (Pusan), (de Gruyter, 1995), 69–105.Google Scholar
[15]Fricke, R. and Klein, F.. Vorlesungen über die Theorie der Automorphen Funktionen. Vol. 1 (Teubner, 1897).Google Scholar
[16]Griffiths, D.. Length inequalities for systems of geodesic loops on a surface of genus two. Bull. London Math. Soc. 28 (1996), 505–508.Google Scholar
[17]Griffiths, D.. The side-pairing elements of Maskit's fundamental domain for the modular group in genus two. Ann. Acad. Sci. Fenn. Math. 26 (2001), 3–50.Google Scholar
[18]Haas, A.. Length spectra as moduli for hyperbolic surfaces. Duke Math. J. 52 (1985), 923–934.CrossRefGoogle Scholar
[19]Hejhal, D.. The Selberg trace formula for PSL (2, R), vol. 1. Lecture Notes in Math., vol. 548, (Springer-Verlag, 1976).Google Scholar
[20]Helling, H.. Diskrete Untergruppen von SL 2 (R). Invent. Math. 17 (1972), 217–229.Google Scholar
[21]Helling, H.. Über den Raum der kompakten Riemannschen Fl\"achen vom Geschlecht 2. J. Reine Angew. Math. 268/269 (1974), 286–293.Google Scholar
[22]Horowitz, R. D.. Characters of free groups represented in the two-dimensional special linear group. Comm. Pure Appl. Math. 25 (1972), 635–649.CrossRefGoogle Scholar
[23]Kahlia, R. N. and Rosenberger, G.. Automorphisms of the Fuchsian groups of type (0;2,2,2,q;0). Comm. Algebra 11 (1978), 1115–1129.Google Scholar
[24]Lehner, J.. On polygon groups, in: Analytic Number Theory (Philadelphia, 1980). Lecture Notes in Math., vol. 899, pp. 315–324 (Springer-Verlag, 1981).CrossRefGoogle Scholar
[25]Maclachlan, C. and Reid, A.. The arithmetic of hyperbolic 3-manifolds. Graduate Texts in Mathematics (Springer-Verlag, New York, 2003).Google Scholar
[26]Maclachlan, C. and Rosenberger, G.. Small volume isospectral, non-isometric, hyperbolic 2-orbifolds. Arch. Math. 62 (1994), 33–37.CrossRefGoogle Scholar
[27]Maskit, B.. Kleinian groups. Grundlehren der Mathematischen Wissenschaften, vol 287 (Springer-Verlag, 1988).CrossRefGoogle Scholar
[28]Maskit, B.. A picture of moduli space. Invent. Math. 126 (1996), 341–390.Google Scholar
[29]Milnor, J.. On the 3-dimensional Brieskorn manifolds M(p,q,r). Ann. Math. Studies 84 (1975), 175–225.Google Scholar
[30]Semmler, K.-D.. An explicit fundamental domain for the Teichmüller space of Riemann surfaces of genus 2. Ph.D.thesis, École Polytechnique Fédérale de Lausanne (2000).Google Scholar
[31]Seppälä, M. and Sorvali, T.. Geometry of Riemann surfaces and Teichmüller spaces, vol. 169 North-Holland Mathematics Studies (North-Holland Publishing Co., 1992).Google Scholar
[32]Singerman, D.. Finitely maximal Fuchsian groups. J. London Math. Soc. 6 (1972), 29–38.CrossRefGoogle Scholar
[33]Sunada, T.. Riemannian coverings and isospectral manifolds. Ann. of Math. 121 (1985), 169–186.Google Scholar
[34]Tse, R. M.. A lower bound for the number of isospectral surfaces; in: Recent developments in geometry (Los Angeles, 1987), pp. 161–164 (Amer. Math. Soc., 1989).CrossRefGoogle Scholar
[35]Vignéras, M.-F.. Variétés riemanniennes isospectrales et non isométriques. Ann. of Math. 112 (1980), 21–32.Google Scholar
[36]Vignéras, M.-F.. Arithmétique des algè;bres de quaternions. Lecture Notes in Math., vol. 800 (Springer-Verlag, 1980).Google Scholar