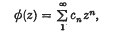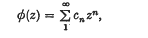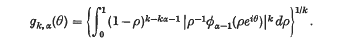Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Flett, Thomas Muirhead
1960.
A note on maximal function.
Tohoku Mathematical Journal,
Vol. 12,
Issue. 1,
Flett, T. M.
1972.
Some inequalities for a hypergeometric integral.
Proceedings of the Edinburgh Mathematical Society,
Vol. 18,
Issue. 1,
p.
31.
Jevtić, Miroljub
Vukotić, Dragan
and
Arsenović, Miloš
2016.
Taylor Coefficients and Coefficient Multipliers of Hardy and Bergman-Type Spaces.
Vol. 2,
Issue. ,
p.
247.