Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T01:15:13.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Some stability properties of c0-saturated spaces

Published online by Cambridge University Press:  24 October 2008

Denny H. Leung
Denny H. Leung
Affiliation:
Department of Mathematics, National University of Singapore, Singapore 0511 e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Banach space is c0-saturated if all of its closed infinite-dimensional subspaces contain an isomorph of c0. In this article, we study the stability of this property under the formation of direct sums and tensor products. Some of the results are: (1) a slightly more general version of the fact that c0-sums of c0-saturated spaces are c0-saturated; (2) C(K, E) is c0-saturated if both C(K) and E are; (3) the tensor product 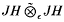is c0-saturated, where JH is the James Hagler space

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 118 , Issue 2 , September 1995 , pp. 287 - 301
Copyright
Copyright © Cambridge Philosophical Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1[Elton, J.. Extremely weakly unconditionally convergent series. Israel J. Math. 40 (1981), 255–258.CrossRefGoogle Scholar
[2[Fonf, V. F.. On a property of Lindenstrauss-Phelps spaces. Funct. Anal. Appl. 13 (1979), 79–80 (translated from Russian).CrossRefGoogle Scholar
[3[Fonf, V. F.. Polyhedral Banach spaces. Mat. Zam. 30 (1981), 627–634 (translated from Russian).Google Scholar
[4[Hagler, James. A counterexample to several questions about Banach spaces. Studia Math. 60 (1977), 289–308.Google Scholar
[5[Knaust, H. and Odell, E.. On c 0-sequences in Banach spaces. Israel J. Math. 67 (1989), 153–169.CrossRefGoogle Scholar
[6[Leung, Denny H.. Embedding l 1 into tensor products of Banach spaces. Functional Analysis (eds. Odell, E. and Rosenthal, H.), Lecture Notes in Math., vol. 1470 (Springer-Verlag, 1991), 171–176.CrossRefGoogle Scholar
[7[Lindenstrauss, Joram and Tzafrihi, Lior. Classical Banach spaces I, sequence spaces (Springer-Verlag, 1977).Google Scholar
[8[Rosenthal, H.. A characterization of Banach spaces containing l 1. Proc. Nat. Acad. Sci. (U.S.A.) 71 (1974), 2411–2413.CrossRefGoogle Scholar
[9[Rosenthal, H.. Class notes. Topics course in analysis (University of Texas).Google Scholar
[10[Rosenthal, H.. Some aspects of the subspace structure of infinite dimensional Banach spaces; in Approximation Theory and Functional Analysis (ed. Chuy, C.) (Academic Press, 1990).Google Scholar
[11[Ruess, W.. Duality and geometry of spaces of compact operators; in Functional Analysis: Surveys and Recent Results III (ed. Bierstedt, K.-D. and Fuchssteiner, B.). Math. Studies, no. 90 (North-Holland, Amsterdam, 1985), 59–78.Google Scholar
[12[Schaefer, H. H.. Banach lattices and positive operators (Springer-Verlag, 1974).CrossRefGoogle Scholar
[13[Semadeni, Z.. Banach spaces of continuous functions I. Monografie Matematyczne (PWN-Polish Scientific Publishers 55, 1971).Google Scholar