Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T00:50:40.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Some results on generalized hypergeometric polynomials†

Published online by Cambridge University Press:  24 October 2008

Manilal Shah
Manilal Shah
Affiliation:
Department of Mathematics, P.M.B.G. College, Indore (M.P.), India
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, using a generalized hypergeometric polynomial defined by

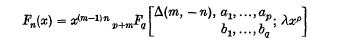
where Δ(m, − n) denotes the set of m-parameters:

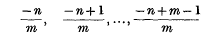
and m, n are positive integers, we have established some infinite series, transformations, integrals and expansion formulae for generalized hypergeometric polynomials. The polynomial is in a generalized form which yields many known polynomials with proper choice of parameters. Special cases have also been given.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 66 , Issue 1 , July 1969 , pp. 95 - 104
Copyright
Copyright © Cambridge Philosophical Society 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1Erdélyi, A. et al. Higher transcendental functions, vol. I (McGraw-Hill; New York, 1953).Google Scholar
2Erdélyi, A. et al. Tables of integral transforms, vol. II (McGraw-Hill; New York, 1954).Google Scholar
3Fasenmyer, Sister M. Celine. Some generalized hypergeometric polynomials. Bull. Amer. Math. Soc. 53 (1947), 806–812.CrossRefGoogle Scholar
4Jet, Wimp and Yudell, L. Luke. Expansion formulas for generalized hypergeometric functions. Rend. Circ. Mat. Palermo, 11 (1962), 351–366.Google Scholar
5Macrobert, T. M.Functions of a complex variable (London Macmillan and Co.; New York, 1958).Google Scholar
6Rainville, E. D.Special functions (Macmillan Company; New York, 1960).Google Scholar
7Shah, Mantlal. Certain integrals involving the product of two generalized hypergeometric polynomials. Proc. Nat. Acad. Sci. India Sect. A 37 (1967), 79–96.Google Scholar
(8)Shah, Manilal. Expansion formula for a generalized hypergeometric polynomial in series of Jacobi polynomial. I. Matematiche (Catania), communicated for publication.Google Scholar
(9)Shah, Manilal. Expansion formula for a generalized hypergeometric polynomial in series of Jacobi polynomial. II. Boll. Un. Mat. Ital., communicated for publication.Google Scholar