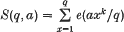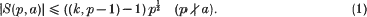Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Гараев, Мубарис Зафар оглы
and
Garaev, Mubaris Zafar ogly
2000.
О тригонометрической сумме Гаусса.
Математические заметки,
Vol. 68,
Issue. 2,
p.
173.
Garaev, M. Z.
2000.
On the gauss trigonometric sum.
Mathematical Notes,
Vol. 68,
Issue. 2,
p.
154.
Cochrane, Todd
and
Zheng, Zhiyong
2001.
On upper bounds of Chalk and Hua for exponential sums.
Proceedings of the American Mathematical Society,
Vol. 129,
Issue. 9,
p.
2505.
Patterson, S. J.
2003.
The Asymptotic Distribution of Exponential Sums, I.
Experimental Mathematics,
Vol. 12,
Issue. 2,
p.
135.
Bourgain, J.
2009.
On the distribution of the residues of small multiplicative subgroups of
$$
\mathbb{F}_p
$$
.
Israel Journal of Mathematics,
Vol. 172,
Issue. 1,
p.
61.
Гараев, Мубарис Зафар оглы
and
Garaev, Mubaris Zafar ogly
2010.
Суммы и произведения множеств и оценки рациональных тригонометрических сумм в полях простого порядка.
Успехи математических наук,
Vol. 65,
Issue. 4,
p.
5.
Bourgain, Jean
2010.
Additive Number Theory.
p.
9.
Bourgain, J.
2010.
Estimates on polynomial exponential sums.
Israel Journal of Mathematics,
Vol. 176,
Issue. 1,
p.
221.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
195.
Bourgain, Jean
2013.
Erdős Centennial.
Vol. 25,
Issue. ,
p.
111.
Demirci Akarsu, Emek
and
Marklof, Jens
2013.
THE VALUE DISTRIBUTION OF INCOMPLETE GAUSS SUMS.
Mathematika,
Vol. 59,
Issue. 2,
p.
381.
Lewko, Mark
O’Neill, Adam
and
Smith, Adam
2013.
Advances in Cryptology – EUROCRYPT 2013.
Vol. 7881,
Issue. ,
p.
55.
Астахов, Василий Вадимович
and
Astakhov, Vasilii Vadimovich
2013.
О существовании и числе стационарных точек дискретного логарифма по основанию, отличному от первообразного корня.
Дискретная математика,
Vol. 25,
Issue. 4,
p.
41.
Demirci Akarsu, Emek
2014.
Short incomplete Gauss sums and rational points on metaplectic horocycles.
International Journal of Number Theory,
Vol. 10,
Issue. 06,
p.
1553.
Alon, Noga
and
Bourgain, Jean
2014.
Additive Patterns in Multiplicative Subgroups.
Geometric and Functional Analysis,
Vol. 24,
Issue. 3,
p.
721.
Smith, Adam
and
Zhang, Ye
2015.
Theory of Cryptography.
Vol. 9014,
Issue. ,
p.
609.
Cochrane, Todd
Ostergaard, Misty
and
Spencer, Craig
2022.
Homogeneous additive congruences.
Rocky Mountain Journal of Mathematics,
Vol. 52,
Issue. 4,
Garaev, Moubariz Z.
and
Shparlinski, Igor E.
2023.
On the distribution of modular inverses from short intervals.
Mathematika,
Vol. 69,
Issue. 4,
p.
1183.