Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T13:37:03.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular measures with absolutely continuous convolution squares

Published online by Cambridge University Press:  24 October 2008

Edwin Hewitt  and
Herbert S. Zuckerman
Edwin Hewitt
Affiliation:
University of Washington, Seattle, U.S.A.
Herbert S. Zuckerman
Affiliation:
University of Washington, Seattle, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Introduction. A famous construction of Wiener and Wintner ((13)), later refined by Salem ((11)) and extended by Schaeffer ((12)) and Ivašev-Musatov ((8)), produces a non-negative, singular, continuous measure μ on [ − π,π[ such that

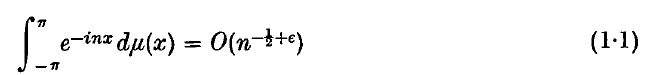
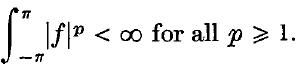for every ∈ > 0. It is plain that the convolution μ * μ is absolutely continuous and in fact has Lebesgue–Radon–Nikodým derivative f such that For general locally compact Abelian groups, no exact analogue of (1 · 1) seems possible, as the character group may admit no natural order. However, it makes good sense to ask if μ* μ is absolutely continuous and has pth power integrable derivative. We will construct continuous singular measures μ on all non-discrete locally compact Abelian groups G such that μ * μ is a absolutely continuous and for which the Lebesgue–Radon–Nikodým derivative of μ * μ is in, 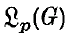for all real p > 1.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 3 , July 1966 , pp. 399 - 420
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Edwards, R. E. and Hewitt, E.Pointwise limits for sequences of convolution operators. Acta Math. 113 (1965), 181–218.CrossRefGoogle Scholar
(2)Glicksberg, I.Fourier–Stieltjes transforms with small supports. Illinois J. Math. 9 (1965), 418–427.CrossRefGoogle Scholar
(3)Hewitt, E. and Kakutani, S.A class of multiplicative linear functionals on the measure algebra of a locally compact Abelian group. Illinois J. Math. 4 (1960), 553–574.CrossRefGoogle Scholar
(4)Hewitt, E. and Kakutani, S.Some multiplicative linear functionals on M(G). Ann. of Math. (2), 79 (1964), 489–505.CrossRefGoogle Scholar
(5)Hewitt, E. and Ross, K. A.Abstract harmonic analysis, Vol. i (Springer-Verlag; Heidelberg, 1963).Google Scholar
(6)Hewitt, E. and Stromberg, K. R.A remark on Fourier-Stieltjes transforms. An. Acad. Brasil Ci. 34 (1962), 175–180.Google Scholar
(7)Hewitt, E. and Stromberg, K. R.Real and abstract analysis (Springer-Verlag; Heidelberg and New York, 1965).Google Scholar
(8)Ivašev-Musatov, O. S.On coefficients of trigonometric null-series. Izv. Akad. Nauk SSSR, Ser. Mat. 21 (1957), 559–578.Google Scholar
(9)Littlewood, J. E.On the Fourier coefficients of functions of bounded variation. Quarterly J. Math. (2), 7 (1936), 219–226.CrossRefGoogle Scholar
(10)Men'šov, D. E.Sur l'unicité du développement trigonométrique. C.R. Acad. Sci., Paris, 163 (1916), 433–436.Google Scholar
(11)Salem, R.On singular monotonic functions of the Cantor type. J. Math. Phys. 21 (1942), 69–82.CrossRefGoogle Scholar
(12)Schaeffer, A. C.The Fourier–Stieltjes coefficients of a function of bounded variation. Amer. J. Math. 61 (1939), 934–940.CrossRefGoogle Scholar
(13)Wiener, N. and Wintner, A.Fourier–Stieltjes transforms and singular infinite convolutions. Amer. J. Math. 60 (1938), 513–522.CrossRefGoogle Scholar
(14)Zygmund, A.Trigonometric series (2nd edition, two vols.; Cambridge University Press, 1959).Google Scholar