Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T23:14:13.519Z Has data issue: false hasContentIssue false
  • English
  • Français

The restricted Burnside problem for Moufang loops

Part of: Other nonassociative rings and algebras Other generalizations of groups

Published online by Cambridge University Press:  16 July 2021

ALEXANDER GRISHKOV ,
LIUDMILA SABININA  and
EFIM ZELMANOV
ALEXANDER GRISHKOV
Affiliation:
Department of Mathematics, University of São Paulo, Caixa Postal 66281, São Paulo-SP, 05311-970, Brazil. Omsk F.M. Dostoevsky State University, Neftezavodskaya 11, Omsk, Omskaya obl., 644053, Russia. e-mail: [email protected]
LIUDMILA SABININA*
Affiliation:
Department of Mathematics, Autonomous University of the State of Morelos, Avenida Universidad 1001, Cuernavaca, 62209Morelos, Mexico. e-mail: [email protected]
EFIM ZELMANOV
Affiliation:
Department of Mathematics, University of California, San Diego, 9500 Giman Dr. La Jolla, California 92093-0112, U.S.A. e-mail: [email protected]
*
†Corresponding author
Get access Rights & Permissions [Opens in a new window]

Abstract

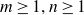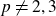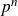We prove that for positive integers $m \geq 1, n \geq 1$ and a prime number $p \neq 2,3$ there are finitely many finite m-generated Moufang loops of exponent $p^n$ .

MSC classification

Primary: 20N05: Loops, quasigroups
Secondary: 17D10: Mal'cev (Mal'tsev) rings and algebras
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 1 , July 2022 , pp. 201 - 211
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to the memory of Peter Plaumann

References

Bruck, R. H.. A survey of binary systems, vol. 20, (Springer, 1971).CrossRefGoogle Scholar
Dixon, J. D., du Sautoy, M. P. F., Mann, A., and Segal, D.. Analytic pro-p groups, second ed., Cambridge Studies in Advanced Math., no. 61, (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
Doro, S.. Simple Moufang loops. Math. Proc. Camb. Phil. Soc. 83 (1978), no. 3, 377–392.Google Scholar
Filippov, V. T.. The Engel algebras of Malcev. Algebra and Logic 15 (1976), no. 1, 89–109.Google Scholar
Glauberman, G.. On loops of odd order. II. J. Algebra 8 (1968), 393–414.CrossRefGoogle Scholar
Grishkov, A. N.. The weakened Burnside problem for Moufang loops of prime period. Sibirsk. Mat. Zh. 28 (1987), no. 3, 60–65, 222.Google Scholar
Grishkov, A.. Lie algebras with triality. J. Algebra 266 (2003), no. 2, 698–722.Google Scholar
Grishkov, A. N. and Zavarnitsine, A. V.. Lagrange’s theorem for Moufang loops. Math. Proc. Cambridge Philos. Soc. 139 (2005), no. 1, 41–57.Google Scholar
Grishkov, A. N. and Zavarnitsine, A. V.. Groups with triality. J. Algebra Appl. 5 (2006), no. 4, 441–463.Google Scholar
Grishkov, A. N. and Zavarnitsine, A. V.. Sylow’s theorem for Moufang loops. J. Algebra 321 (2009), no. 7, 1813–1825.Google Scholar
Higman, G.. Lie ring methods in the theory of finite nilpotent groups Proc. Internat. Congress Math. 1958. (Cambridge Univ. Press, New York, 1960), pp. 307–312.Google Scholar
Jacobson, N.. Lie algebras. Interscience Tracts in Pure and Applied Math., no. 10, (Interscience Publishers, New York-London, 1962).Google Scholar
Kostrikin, A. I.. On Lie rings satisfying the Engel condition. Dokl. Akad. Nauk SSSR (N.S.) 108 (1956), 580–582.Google Scholar
Kuzmin, E. N.. Structure and representations of finite dimensional Malcev algebras. Quasigroups Related Systems 22 (2014), no. 1, 97–132.Google Scholar
Nagy, G. P.. Burnside problems for Moufang and Bol loops of small exponent. Acta Sci. Math. (Szeged) 67 (2001), no. 3-4, 687–696.Google Scholar
Plaumann, P. and Sabinina, L.. On nuclearly nilpotent loops of finite exponent. Comm. Algebra 36 (2008), no. 4, 1346–1353.Google Scholar
Plaumann, P. and Sabinina, L.. Some remarks on the Burnside problem for loops, Advances in Algebra and Combinatorics, (World Sci. Publ., Hackensack, NJ, 2008), pp. 293–302.CrossRefGoogle Scholar
Plotkin, B. I.. Algebraic sets of elements in groups and Lie algebras. Uspehi Mat. Nauk 13 (1958), no. 6 (84), 133-138.Google Scholar
Stitzinger, E. L.. On nilpotent and solvable Malcev algebras. Proc. Amer. Math. Soc. 92 (1984), no. 2, 157–163.Google Scholar
Zelmanov, E. I.. Solution of the restricted Burnside problem for groups of odd exponent. Izv. Akad. Nauk SSSR Ser. Mat. 54 (1990), no. 1, 42–59, 221.Google Scholar
Zelmanov, E. I.. Solution of the restricted Burnside problem for 2-groups. Mat. Sb. 182 (1991), no. 4, 568–592.Google Scholar
Zelmanov, E.. Nil rings and periodic groups. KMS Lecture Notes in Mathematics. (Korean Mathematical Society, Seoul, 1992).Google Scholar
Zhevlakov, K. A., Slinko, A. M., Shestakov, I. P., and Shirshov, A. I.. Rings that are nearly associative. Pure Appl. Math., vol. 104, (Academic Press, Inc., New York-London, 1982).Google Scholar