Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T02:01:39.146Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on the Dirac δ-operator

Published online by Cambridge University Press:  24 October 2008

Hans Ludwig Hamburger
Hans Ludwig Hamburger
Affiliation:
Fen FakültesiUniversity of Ankara, Turkey
Get access Rights & Permissions [Opens in a new window]

Extract

1. In this note we shall prove the

Theorem 1. Let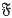be a linear space of (real or complex) functions f(s) defined in the interval 0 ≤ s ≤ 1 subject to the following two conditions:

(i) every function of the infinite sequence 1, s, s2, …, sn, … is an element of;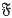

(ii) two elements, f(s) and g(s), of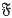are to be considered as distinct if, and only if, they differ on a set of positive measure in the interval 0 ≤ s ≤ 1.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 45 , Issue 4 , October 1949 , pp. 489 - 494
Copyright
Copyright © Cambridge Philosophical Society 1949

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Aronszajn, N.Proc. Cambridge Phil. Soc. 39 (1943), 133–53.CrossRefGoogle Scholar
(2)Dirac, P. A. M.The Principles of Quantum Mechanics, 1st ed. (Oxford, 1930).Google Scholar
(3)Dirac, P. A. M.The Principles of Quantum Mechanics, 3rd ed. (Oxford, 1947).Google Scholar
(4)Hamburger, H. L.Math. Z. 4 (1919), 186–222.CrossRefGoogle Scholar
(5)Lebesgue, H.Ann. Fac. Sci. Toulouse, Sér. 3, 1 (1909), 25–118.Google Scholar
(6)Lerch, M.Acta Math. 27 (1903), 339–51.CrossRefGoogle Scholar
(7)von Neumann, J.Mathematische Grundlagen der Quantenmechanik (Berlin, 1932).Google Scholar
(8)von Neumann, J. Charakterisierung des Spektrums eines Integraloperators. Actualités sci. industr. 229 (Paris, 1935).Google Scholar
(9)Weyl, H.Math. Ann. 66 (1909), 273–324.CrossRefGoogle Scholar