Reflections in extended Bianchi groups
Published online by Cambridge University Press: 24 October 2008
Extract
Let d be a positive square-free number. Let Od be the ring of integers in Q(√ −d). The groups PSL(2, Od) are called collectively the Bianchi groups. The extended Bianchi group Bd is the maximal discrete extension of PSL(2, Od) in PSL(2, C). The group Bd acts by linear fractional transformations on the complex plane C. Let RBd be Bd with the generator θ, 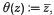 , adjoined. (RBd will be also called an extended Bianchi group (cf. [18])). A group is said to be reflective if it contains a Coxeter subgroup (i.e. a subgroup generated by reflections) of finite index. The groups RBd and their subgroups have been investigated in [3, 6, 13, 15, 16, 17, 18, 20, 21]. In 1892 Bianchi[3] proved that PGL(2, Od)⋊{θ} is reflective if d ≤ 19, d ╪ 14 or 17. Vinberg [18] proved that if the group RBd is reflective, then the orders of all elements of the ideal-class group of the field Q(√ −d) should divide 4. Shaiheev [16] proved that there are only finitely many reflective extended Bianchi groups and found all of them for d ≤ 30. Similar results are obtained for groups PGL(2, Od) ⋊ {θ} which, as Shvartsman [17] showed, are reflective only when d = 1, 2, 5, 6, 10, 13, 21, provided d = 1 or 2 (mod 4).
, adjoined. (RBd will be also called an extended Bianchi group (cf. [18])). A group is said to be reflective if it contains a Coxeter subgroup (i.e. a subgroup generated by reflections) of finite index. The groups RBd and their subgroups have been investigated in [3, 6, 13, 15, 16, 17, 18, 20, 21]. In 1892 Bianchi[3] proved that PGL(2, Od)⋊{θ} is reflective if d ≤ 19, d ╪ 14 or 17. Vinberg [18] proved that if the group RBd is reflective, then the orders of all elements of the ideal-class group of the field Q(√ −d) should divide 4. Shaiheev [16] proved that there are only finitely many reflective extended Bianchi groups and found all of them for d ≤ 30. Similar results are obtained for groups PGL(2, Od) ⋊ {θ} which, as Shvartsman [17] showed, are reflective only when d = 1, 2, 5, 6, 10, 13, 21, provided d = 1 or 2 (mod 4).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 13 - 25
- Copyright
- Copyright © Cambridge Philosophical Society 1994
References
REFERENCES
- 8
- Cited by


