Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T13:48:02.574Z Has data issue: false hasContentIssue false
  • English
  • Français

A reduction theory of second order meromorphic differential equations, I

Published online by Cambridge University Press:  24 October 2008

W. B. Jurkat  and
H. J. Zwiesler
W. B. Jurkat
Affiliation:
Department of Mathematics, Syracuse University, Syracuse, NY 13244, U.S.A.
H. J. Zwiesler
Affiliation:
Abteilung Mathematik, Universität Ulm, D 7900 Ulm, West Germany
Get access Rights & Permissions [Opens in a new window]

Extract

In this article we investigate the meromorphic differential equation X′(z) = A(z) X(z), often abbreviated by [A], where A(z) is a matrix (all matrices we consider have dimensions 2 × 2) meromorphic at infinity, i.e. holomorphic in a punctured neighbourhood of infinity with at most a pole there. Moreover, X(z) denotes a fundamental solution matrix. Given a matrix T(z) which together with its inverse is meromorphic at infinity (a meromorphic transformation), then the function Y(z) = T−1(z) X(z) solves the differential equation [B] with B = T−1AT − T−1T [1,5]. This introduces an equivalence relation among meromorphic differential equations and leads to the question of finding a simple representative for each equivalence class, which, for example, is of importance for further function-theoretic examinations of the solutions. The first major achievement in this direction is marked by Birkhoff's reduction which shows that it is always possible to obtain an equivalent equation [B] where B(z) is holomorphic in ℂ ¬ {0} (throughout this article A ¬ B denotes the difference of these sets) with at most a singularity of the first kind at 0 [1, 2, 5, 6]. We call this the standard form. The question of how many further simplifications can be made will be answered in the framework of our reduction theory. For this purpose we introduce the notion of a normalized standard equation [A] (NSE) which is defined by the following conditions:

(i) 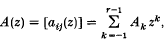, where r ∈ ℕ and Ak are constant matrices, (notation: )

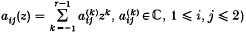(ii) A(z) has trace tr 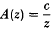for some c ∈ ℂ,

(iii) Ar−1 has different eigenvalues,

(iv) the eigenvalues of A−1 are either incongruent modulo 1 or equal,

(v) if A−1 = μI, then Ar−1 is diagonal,

(vi) Ar−1 and A−1 are triangular in opposite ways,

(vii) a12(z) is monic (leading coefficient equals 1) unless a12 ≡ 0; furthermore a21(z) is monic in case that a12 ≡ 0 but a21 ≢ 0.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 101 , Issue 2 , March 1987 , pp. 323 - 342
Copyright
Copyright © Cambridge Philosophical Society 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balser, W., Jurkat, W. B. and Lutz, D. A.. A general theory of invariants for meromorphic differential equations. I. Formal invariants, Funk. Ekvac. 22 (1979), 197–221.Google Scholar
[2]Coddington, E. A. and Levinson, N.. Theory of Ordinary Differential Equations (McGraw-Hill, 1955).Google Scholar
[3]Gantmacher, F. R.. Theory of Matrices, vol. I (Chelsea, 1959).Google Scholar
[4]Hurewicz, W. and Wallman, H.. Dimension Theory (Princeton University Press, 1948).Google Scholar
[5]Jurkat, W. B.. Meromorphe Differentialgleichungen, Lecture Notes in Math. No. 637 (Springer, 1978).CrossRefGoogle Scholar
[6]Jurkat, W. B., Lutz, D. A. and Peyerimhoff, A.. Birkhoff invariants and effective calculations for meromorphic linear differential equations, I. Jour. Math. Anal. Appl. 53 (1976), 438–470.CrossRefGoogle Scholar
[7]Rogers, C. A.. Hausdorff Measures (Cambridge University Press, 1970).Google Scholar
[8]Saks, S.. Theory of The Integral (G. E. Stechert, 1937).Google Scholar
[9]van der Waerden, B. L.. Algebra, vol. 1 (Ungar, 1970).Google Scholar
[10]Wasow, W.. Asymptotic Expansions for Ordinary Differential Equations (John Wiley & Sons, 1965).Google Scholar