Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
RIEGER, J. H.
RUAS, M. A. S.
and
ATIQUE, R. WIK
2008.
M-deformations of -simple germs from to.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 144,
Issue. 1,
p.
181.
Domitrz, W.
and
Rieger, J. H.
2009.
Volume preserving subgroups of $${{\mathcal A}}$$ and $${{\mathcal K}}$$ and singularities in unimodular geometry.
Mathematische Annalen,
Vol. 345,
Issue. 4,
p.
783.
Barbosa, Grazielle Feliciani
Martins, Rodrigo
and
Saia, Marcelo José
2012.
Topology of simple singularities of ruled surfaces in Rp.
Topology and its Applications,
Vol. 159,
Issue. 2,
p.
397.
Oset Sinha, R.
Ruas, M. A. S.
and
Wik Atique, R.
2014.
Classifying codimension two multigerms.
Mathematische Zeitschrift,
Vol. 278,
Issue. 1-2,
p.
547.
Rodrigues Hernandes, M E
and
Ruas, M A S
2019.
Parametrized monomial surfaces in 4-space.
The Quarterly Journal of Mathematics,
Vol. 70,
Issue. 2,
p.
473.
Nuño-Ballesteros, Juan J.
and
Mendes, Rodrigo
2020.
Topological Classification and Finite Determinacy of Knotted Maps.
Michigan Mathematical Journal,
Vol. 69,
Issue. 4,
Peñafort Sanchis, Guillermo
2020.
Reflection maps.
Mathematische Annalen,
Vol. 378,
Issue. 1-2,
p.
559.
Breva Ribes, I.
and
Oset Sinha, R.
2022.
Simplicity of Augmentations of Codimension 1 Germs and by Morse Functions.
Mediterranean Journal of Mathematics,
Vol. 19,
Issue. 6,
Rodrigues Hernandes, M E
and
Ruas, M A S
2023.
Join operation and A-finite map-germs.
The Quarterly Journal of Mathematics,
Vol. 74,
Issue. 4,
p.
1415.
Moya-Pérez, J. A.
and
Nuño-Ballesteros, J. J.
2024.
Topology of Fold Map Germs from $$\mathbb R^3$$ to $$\mathbb R^5$$.
Mediterranean Journal of Mathematics,
Vol. 21,
Issue. 1,


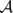 -simple map-germs from
-simple map-germs from 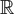
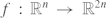 are isolated transverse double-points. All
are isolated transverse double-points. All 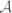 -simple germs
-simple germs 