Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T01:00:18.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasifree representations of Clifford algebras

Published online by Cambridge University Press:  24 October 2008

P. L. Robinson
P. L. Robinson
Affiliation:
Department of Mathematics, University of Florida, Gainesville, FL 32611, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Let V be an infinite-dimensional real Hilbert space with associated C* Clifford algebra C[V]. To any state σ of the C* algebra C[V] there corresponds a skew-adjoint operator C of norm at most unity on V such that

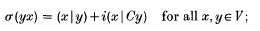
we refer to C as the covariance of the state σ.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 113 , Issue 3 , May 1993 , pp. 487 - 497
Copyright
Copyright © Cambridge Philosophical Society 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Araki, H.. On quasifree states of CAR and Bogoliubov automorphisms. Publ. Res. Inst.Math. Sci. 6 (1970/1901), 386–442.CrossRefGoogle Scholar
[2]Araki, H.. Bogoliubov automorphisms and Fock representations of canonical anti-commutation relations. In Operator Algebras and Mathematical Physics, Contemporary Math. no. 62 (American Mathematical Society, 1987), pp. 23–141.CrossRefGoogle Scholar
[3]Balslev, E., Manuceau, J. and Verbeure, A.. Representations of anticommutation relations. Comm. Math. Phys. 8 (1968), 315–326.CrossRefGoogle Scholar
[4]Bratteli, O. and Robinson, D. W.. Operator Algebras and Quantum Statistical Mechanics II. Texts and Monographs in Physics (Springer-Verlag, 1981).CrossRefGoogle Scholar
[5]De La Harpe, P. and Plymen, R. J.. Automorphic group representations: a new proof of Blattner's theorem. J. London Math. Soc. (2) 19 (1979), 509–522.CrossRefGoogle Scholar
[6]Hannabuss, K. C.. KMS states for reduced groups, theta functions and the Powers–Størmer construction. Math. Proc. Cambridge Philos. Soc. 105 (1989), 397–410.CrossRefGoogle Scholar
[7]Shale, D. and Stinespring, W. F.. States of the Clifford algebra. Ann. of Math. 80 (1964), 365–381.CrossRefGoogle Scholar
[8]van Daele, A.. Quasi-equivalence of quasi-free states on the Weyl algebra. Comm. Math. Phys. 21 (1971), 171–191.CrossRefGoogle Scholar