Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T13:11:51.881Z Has data issue: false hasContentIssue false
  • English
  • Français

The quasi-centre of a Banach algebra

Published online by Cambridge University Press:  24 October 2008

J. F. Rennison
J. F. Rennison
Affiliation:
Mathematical Institute, University of Kent, Canterbury
Get access Rights & Permissions [Opens in a new window]

Extract

An element a of a Banach algebra A over ࠶ will be called quasi-central if, for some K ≥ 1,

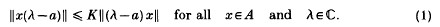
The set Q(A) of all quasi-central elements of A will be called the quasi-centre of A and the set of elements a which satisfy (1) for a particular value of K will be denoted by Q(K, A). The motivation for these definitions is the result of Le Page ([1], proposition 3) that Q(1, A) coincides with the centre Z(A) of A. The reader is referred to [2] and [3] for a study of the properties of quasi-central elements.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 103 , Issue 2 , March 1988 , pp. 333 - 337
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Page, C. Le. Sur quelques conditions entraînant la commutativité dans les algèbres de Banach. C. R. Acad. Sci. Paris Sér. A-B 265 (1967), 235–237.Google Scholar
[2]Rennison, J. F.. Conditions related to centrality in a Banach algebra. J. London Math. Soc. 26, 2 (1982), 155–168.Google Scholar
[3]Rennison, J. F.. Conditions related to centrality in a Banach algebra. II. J. London Math. Soc. 35, (1987), 499–513.Google Scholar