Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T01:40:21.913Z Has data issue: false hasContentIssue false
  • English
  • Français

A quadratic parabolic group

Published online by Cambridge University Press:  24 October 2008

Robert Riley
Robert Riley
Affiliation:
The University, Southampton
Get access Rights & Permissions [Opens in a new window]

Extract

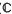When k is a 2-bridge knot with group πK, there are parabolic representations (p-reps) θ: πK → PSL(): = PSL(2, 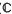). The most obvious problem that this suggests is the determination of a presentation for an image group πKθ. We shall settle the easiest outstanding case in section 2 below, viz. k the figure-eight knot 41, which has the 2-bridge normal form (5, 3). We shall prove that the (two equivalent) p-reps θ for this knot are isomorphisms of πK on πKθ. Furthermore, the universal covering space of S3\k can be realized as Poincaré's upper half space 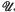3, and πKθ is a group of hyperbolic isometries of 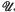3 which is also the deck transformation group of the covering 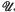3 → S3\k. The group πKθ is a subgroup of two closely related groups that we study in section 3. We shall give fundamental domains, presentations, and other information for all these groups.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 77 , Issue 2 , March 1975 , pp. 281 - 288
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Armstrong, M.The fundamental group of the orbit space of a discontinuous group. Proc. Cambridge Philos. Soc. 64 (1968), 299–301.Google Scholar
(2)Best, L. On discrete subgroups of LF(2, ). Ph.D. thesis, University of Birmingham 1968.Google Scholar
(3)Bianchi, L.Geometrische Darstellung der Gruppen Linearer Substitutionen mit Ganzen Complexen Coefficienten nebst Andwendungen auf die Zahlentheorie. Math. Ann. 38 (1891), 313–333.Google Scholar
(4)Ford, L.Automorphic Functions, 2nd ed. Chelsea (New York 1951).Google Scholar
(5)Maskit, B.On Poincaré's Theorem for Fundamental Polygons. Advances in Math. 7 (1971), 219–230.CrossRefGoogle Scholar
(6)Poincaré, H.Mémoire sur les groupes Kleinéens. Acta Math. 3 (1883), 49–92.Google Scholar
(7)Riley, R.Parabolic representations of knot groups, I. Proc. London Math. Soc. (3) 24 (1972), 217–242.CrossRefGoogle Scholar
(8)Riley, R.Hecke invariants of knot groups. Glasgow Math. J. 15 (1974), 17–26.Google Scholar
(9)Riley, R. Parabolic representations of knot groups, II, submitted for publication.Google Scholar
(10)Swan, R.Generators and Relators for certain Special Linear Groups. Advances in Math. 6 (1971), 1–77.Google Scholar
(11)Waldhausen, F.On irreducible 3-manifolds which are sufficiently large. Ann. of Math. 87 (1968), 56–88.Google Scholar