The Propagation of Radio Waves in an Ionised Atmosphere

Extract

Larmor has shown that if the upper atmosphere contains electrons (charge ε, mass m, density ν) and if collisions between these electrons and molecules—and also the forces between the electrons themselves—are negligible, then electric waves are propagated as if the dielectric constant of the medium were reduced by 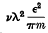, from which it appears that, so long as the approximations are valid, the velocity of propagation of the waves can be increased indefinitely by increasing either the electron density or the wave-length λ. Several later authors have attempted to take account of the collisions between electrons and molecules, assuming free paths or velocities according to Maxwell's laws for a uniform gas, and it appears that the above law holds only for short waves; but it is doubtful how far the properties of a uniform gas can be assumed when periodic forces are acting. In the first part of this paper an alternative method of solution is given by means of Boltzmann's integral equation for a non-uniform gas, the analysis being similar to that used by Lorentz in discussing the motion of free electrons in a metal. Only the case when ν is small is considered, i.e. the interactions of electrons with one another and with positive ions are neglected. How far it is possible to increase the velocity of propagation by increasing ν is a more difficult question, but it seems possible that the forces between the electrons and ions may impose a limit just as collisions with neutral molecules limit the effect of increasing the wave-length.