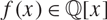Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Li, Ruofan
2023.
Primitive prime divisors in backward orbits.
Journal of Number Theory,
Vol. 245,
Issue. ,
p.
303.
Sadek, Mohammad
Wafik, Mohamed
and
Yesin, Tuğba
2024.
Arithmetic progressions in polynomial orbits.
International Journal of Number Theory,
Vol. 20,
Issue. 08,
p.
2009.