Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-01-09T19:21:20.107Z Has data issue: false hasContentIssue false
  • English
  • Français

The primitive ideal space of the C*-algebra of the affine semigroup of algebraic integers

Published online by Cambridge University Press:  01 October 2012

SIEGFRIED ECHTERHOFF  and
MARCELO LACA
SIEGFRIED ECHTERHOFF
Affiliation:
Mathematisches Institut, Einsteinstr. 62, 48149 Münster, Germany. e-mail: [email protected]
MARCELO LACA
Affiliation:
Department of Mathematics and Statistics, P.O.B. 3060, University of Victoria, Victoria, B.C. CanadaV8W 3R4. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of this paper is to give a complete description of the primitive ideal space of the C*-algebra 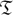[R] associated to the ring of integers R in a number field K in the recent paper [5]. As explained in [5], 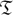[R] can be realized as the Toeplitz C*-algebra of the affine semigroup R ⋊ R× over R and as a full corner of a crossed product C0(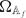) ⋊ K ⋊ K*, where 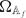is a certain adelic space. Therefore Prim(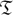[R]) is homeomorphic to the primitive ideal space of this crossed product. Using a recent result of Sierakowski together with the fact that every quasi-orbit for the action of K ⋊ K* on 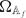contains at least one point with trivial stabilizer we show that Prim(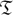[R]) is homeomorphic to the quasi-orbit space for the action of K ⋊ K* on 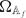, which in turn may be identified with the power set 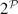of the set of prime ideals 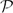of R equipped with the power-cofinite topology.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 154 , Issue 1 , January 2013 , pp. 119 - 126
Copyright
Copyright © Cambridge Philosophical Society 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Archbold, R. J. and Spielberg, J. S.Topologically free actions and ideals in discrete C*-dynamical systems. Proc. Edinburgh Math. Soc. 37 (1994), 119–124.CrossRefGoogle Scholar
[2]Cuntz, J.C*-algebras associated with the ax + b-semigroup over N. Cortiñas, G., (ed.) et al., K-theory and noncommutative geometry. Proceedings of the ICM 2006 satellite conference (Valladolid, Spain, August 31-September 6, 2006). Zürich: European Mathematical Society (EMS). Series of Congress Reports (2008), 201–215.Google Scholar
[3]Cuntz, J. and Li, X.The regular C*-algebra of an integral domain. Clay Mathematics Proceedings 10 (2010), 149–170.Google Scholar
[4]Cuntz, J. and Li, X.C*-algebras associated with integral domains and crossed products by actions on adele spaces. J. Noncommut. Geom. 5 (2011), 1–37.CrossRefGoogle Scholar
[5]Cuntz, J., Deninger, C. and Laca, M. C*-algebras of Toeplitz type associated with algebraic number fields. Math. Ann. (2012), doi: 10.1007/s00208-012-0826-9.CrossRefGoogle Scholar
[6]Dixmier, J.C*-algebras. North-Holland Mathematical Library, Vol. 15 (North-Holland Publishing Co., 1977).Google Scholar
[7]Fell, J. M. G.The dual spaces of C*-algebras. Trans. Amer. Math. Soc. 94 (1960), 365–403.Google Scholar
[8]Guentner, E., Higson, N. and Weinberger, S.The Novikov conjecture for linear groups. Publ. Math. Inst. Hautes Études Sci. 101 (2005), 243–268.CrossRefGoogle Scholar
[9]Gootman, E. C. and Rosenberg, J.The structure of crossed product C*-algebras: a proof of the generalized Effros–Hahn conjecture. Invent. Math. 52 (1979), no. 3, 283–298.CrossRefGoogle Scholar
[10]Green, P.The local structure of twisted covariance algebras. Acta Math. 140 (1978), no. 3-4, 191–250.CrossRefGoogle Scholar
[11]Laca, M. and Raeburn, I.The ideal structure of the Hecke C*-algebra of Bost and Connes. Math. Ann. 318 (2000), 433–451.CrossRefGoogle Scholar
[12]Laca, M. and Raeburn, I.Phase transition on the Toeplitz algebra of the affine semigroup over the natural numbers. Adv. Math. 225 (2010), 643–688.CrossRefGoogle Scholar
[13]Renault, J.The ideal structure of groupoid crossed product C*-algebras. With an appendix by Georges Skandalis. J. Operator Theory 25 (1991), no. 1, 3–36.Google Scholar
[14]Sierakowski, A.The ideal structure of reduced crossed products. Münster J. of Math. 3 (2010), 237–262.Google Scholar