Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T02:22:05.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial conformal tensors

Published online by Cambridge University Press:  24 October 2008

J. C. du Plessis
J. C. du Plessis
Affiliation:
King's College, London
Get access Rights & Permissions [Opens in a new window]

Abstract

The conformal tensors of a Riemannian space Vn are classified and analysed, mainly in terms of the ‘conformal number’ χ which is defined as a certain linear combination of the numbers that characterize the transformation modes of a conformal tensor. In the case of zero rest mass fields (5), χ – 1 is just the spin. Conformal concomitants of the metric tensor and its derivatives up to a finite order m are considered and, in particular, those tensors which are polynomials in the 2nd and higher derivatives of the metric tensor (called conformal P-tensors of order m). The algebraic structure of such a tensor is described by a set of m − 1 integers (S2, …, Sm), referred to as the structure of F and defined in an invariant way in terms of the various polynomial degrees of F and its partial derivatives. The structure of F is related to the m transformation modes of F by the formula: 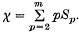. Thus for P-tensors, χ = 0, 2, 3, … and m ≤ χ. The set of structures (S2, …, Sm) of all conformal P-tensors of order less than or equal to m, forms an Abelian monoid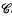 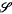m, with addition defined componentwise. In a general V4, it is found that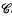 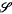4 consists of all triplets (S2, S3, S4) ∈ 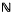3 for which S3 ≤ 4S2. Finally, new conformal P-tensors are constructed so that examples can be given corresponding to every structure in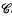 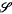4. One also obtains, for each value of χ, a general formula which expresses any conformal P-tensor with conformal number χ in terms of a standard sequence of conformal P-tensors.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 68 , Issue 2 , September 1970 , pp. 329 - 344
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bach, R.Math. Z. 9 (1921), 110.CrossRefGoogle Scholar
(2)du Plessis, J. C.Tensor N. S. 20 (1969), 347.Google Scholar
(3)du Plessis, J. C.Tensor N. S. 21 (1970), 1.Google Scholar
(4)du Plessis, J. C. Preliminary report: Joint Mathematical Colloquium, University of South Africa and University of the Witwatersrand (1969).Google Scholar
(5)Penrose, R.Proc. Roy. Soc. Ser. A 284 (1965), 159.Google Scholar
(6)Penrose, R.Ann. Physics 10 (1960), 171.CrossRefGoogle Scholar
(7)Rund, H.Abh. Math. Sem. Univ. Hamburg 29 (1966), 243.Google Scholar
(8)Schouten, J. A.Ricci-calculus, 2nd ed., Springer-Verlag, Berlin-Göttingen-Heidelberg, (1954).CrossRefGoogle Scholar
(9)Szekeres, P.Proc. Roy. Soc. Ser. A 304 (1968), 113.Google Scholar