Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T13:34:46.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Pestov's identity on frame bundles and applications

Published online by Cambridge University Press:  29 April 2016

MICHELA EGIDI
MICHELA EGIDI*
Affiliation:
Fakultät für Mathematik, Technische Universität Chemnitz, Chemnitz, Germany. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we lift Pestov's Identity on the tangent bundle of a Riemannian manifold M to the bundle of k-tuples of tangent vectors. We also derive an integrated version and a restriction to the frame bundle PkM of k-frames. Finally, we discuss a dynamical application for the parallel transport on 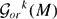$\cal{G}_{or}^{k} (M)$, the Grassmannian of oriented k-planes of M.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 161 , Issue 2 , September 2016 , pp. 357 - 377
Copyright
Copyright © Cambridge Philosophical Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Ainsworth, G. The attenuated magnetic ray transform on surfaces. Inverse. Probl. Imaging 7 (2013), 27–46.CrossRefGoogle Scholar
[2] Alekseevsky, D. V., Cortes, V., Dyckmanns, M. and Mohaupt, T. Quaternionic Kähler metrics associated with special Kähler manifolds. arXiv:1305.3549.Google Scholar
[3] Anikonov, Y. and Romanov, V. On uniqueness of determination of a form of first degree by its integrals along geodesics. J. Inverse Ill-Posed Probl. 5 (1997), 467–480.CrossRefGoogle Scholar
[4] Aravinda, C. S. Curvature vs. Curvature Operator. Special issue of the RMS Newsletter commemorating ICM 2010 in India 19 (2010), 109–118.Google Scholar
[5] Aravinda, C. S. and Farell, T. Nonpositivity: curvature vs curvature operator. Proc. Amter. Math. Soc. 133 (2005), 191–192.CrossRefGoogle Scholar
[6] Ballmann, W. Lectures on Kähler manifolds (European Mathematical Society, 2006).Google Scholar
[7] Berger, M. A Panoramic View of Riemannian Geometry (Springer-Verlag, 2003).Google Scholar
[8] Besse, A. Einstein Manifolds (Springer-Verlag, 1987).Google Scholar
[9] Brin, M. and Gromov, M. On the ergodicity of frame flows. Invent. Math. 60 (1980), 1–7.Google Scholar
[10] Brin, M. and Karcher, H. Frame flows on manifolds with pinched negative curvature. Comp. Math. 52 (3) (1984), 275–297.Google Scholar
[11] Burns, K. and Pollicott, M. Stable ergodicity and frame flows. Geom. Dedicata 98 (2003), 189–210.CrossRefGoogle Scholar
[12] Cortés, V., Dyckmanns, M. and Lindemann, D. Classification of complete projective special real surfaces. Proc. London Math. Soc. 109 (3) (2014), 423–445.CrossRefGoogle Scholar
[13] Cortés, V., Nardmann, M. and Suhr, S. Completeness of hyperbolic centroaffine hypersurfaces. arXiv: 1305.3549.Google Scholar
[14] Croke, C. and Sharafutdinov, V. A. Spectral rigidity of compact negatively curved manifolds. Topology 37 (1998), 1265–1273.CrossRefGoogle Scholar
[15] Dairbekov, N. S. and Paternain, G. P. Longitudinal KAM-cocycles and action spectra of magnetic flows. Math. Res. Lett. 12 (2005), 719–729.Google Scholar
[16] Dairbekov, N. S. and Paternain, G. P. Entropy production in Gaussian thermostats. Comm. Math. Phys. 269 (2007), 533–543.Google Scholar
[17] Dairbekov, N. S. and Paternain, G. P. On the cohomological equation of magnetic flows. Matemática Contemporânea 34 (2008), 155–193.Google Scholar
[18] Dairbekov, N. S. and Paternain, G. P. Rigidity properties of Anosov optical hypersurfaces. Ergodic Theory and Dynam. Systems 28 (2008), 707–737.CrossRefGoogle Scholar
[19] Dairbekov, N. S., Paternain, G. P., Stefanov, P. and Uhlmann, G. The boundary rigidity problem in the presence of a magnetic field. Adv. Math. 216 (2007), 535–609.Google Scholar
[20] Feres, R. Dynamical Systems and Semisimple Groups. An Introduction. (Cambridge University Press, 1998).Google Scholar
[21] Grey, A. A note on manifolds whose holonomy group is a subgroup of Sp(n) ⋅ Sp(1). Michigan Math. J. 16 (2) (1969), 125–128.Google Scholar
[22] Guillemin, V. and Kazhadan, D. Some inverse spectral results for negatively curved 2-manifolds. Topology 19 (1980), 301–312.Google Scholar
[23] Ishihara, S. Quaternian Kählerian manifolds. J. Differential Geometry 9 (1974), 483–500.Google Scholar
[24] Knieper, G. Hyperbolic dynamics and Riemannian geometry in Handbook of Dynamical systems. vol. 1A, 453–545 (North-Holland, 2002).Google Scholar
[25] Knieper, G. A commutator formula for the geodesic flow on a compact Riemannian manifold. pre-print.Google Scholar
[26] Kobayashi, S. and Nomizu, K. Foundations of Differential Geometry, Vol I (Wiley Interscience Publishers, John Wiley and Sons Inc., 1996).Google Scholar
[27] LeBrun, C. A rigidity theorem for Quaternionic-Kähler manifolds. Proc. Amter. Math. Soc. 103 (4) (1988), 1205–1208.Google Scholar
[28] LeBrun, C. On complete quaternionic-Kähler manifolds. Duke Math. J. 63 (3) (1991), 723–743.Google Scholar
[29] Maus, N. Der geodätische Fluss auf symmetrischen Räumen (Diplomarbeit Bochum, 2005).Google Scholar
[30] Min-Oo, M. Spectral rigidity for manifolds with negative curvature operator. In Nonlinear problems in geometry, 99–103. Contemp. Math. 51. (Amer. Math. Soc. 1986).Google Scholar
[31] Paternain, G. P., Salo, M. and Uhlmann, G. Tensor tomography on surfaces. Invent. Math. 193 (2013), 229–247.CrossRefGoogle Scholar
[32] Paternain, G. P., Salo, M. and Uhlmann, G. Tensor tomography: progress and challanges. Chin. Ann. Math. 35B (3) (2014), 399–428.Google Scholar
[33] Pestov, L. N. and Sharafutdinov, V. A. Integral Geometry of tensor fields on a manifold of negative curvature. (Russian) Sibirsk. Mat. Zh. 29 (3) (1988), 114–130, 221; translation in Siberian Math. J. 29 (3) (1988), 427–441.Google Scholar
[34] Sharafutdinov, V. A. Integral Geometry of Tensor Fields (VSP, 1994).Google Scholar