Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T13:25:19.663Z Has data issue: false hasContentIssue false
  • English
  • Français

Permanent of the product of doubly stochastic matrices

Published online by Cambridge University Press:  24 October 2008

R. A. Brualdi
R. A. Brualdi
Affiliation:
University of Wisconsin
Get access Rights & Permissions [Opens in a new window]

Extract

If A = [aij] is an n × n matrix, the permanent of A is the scalar valued function of A defined by

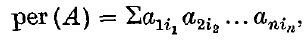
where the summation extends over all permutations (i1, i2, …, in) of the integers 1, 2, …, n. If we assume that A is a non-negative matrix (that is, that A has non-negative entries) then we come upon an extremely interesting situation. Much work has been done in finding significant upper bounds for the permanent and permanental minors of A (see, e.g. (2, 4–7) in (5) an excellent bibliography is given). If B = [bij] is another n × n non-negative matrix, then we may form the product AB and consider the permanent of this matrix. Unlike the determinant, the permanent is not a multiplicative function. In our circumstances here, however, it is easy to verify and indeed a proof was written down in (1) that

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 4 , October 1966 , pp. 643 - 648
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Brualdi, R. A.Permanent of the direct product of matrices. Pacific J. Math. 16 (1966), 471–482.CrossRefGoogle Scholar
(2)Brualdi, R. A. & Newman, M.Inequalities for permanents and permanental minors. Proc. Cambridge Philos. Soc. 61 (1965), 741–746.CrossRefGoogle Scholar
(3)Dulmage, A. L. & Mendelsohn, N. S.Coverings of bipartite graphs. Canad. J. Math. 10 (1958), 517–534.CrossRefGoogle Scholar
(4)Jurkat, W. B. & Ryser, H. J.Matrix factorizations of determinants and permanents. J. Algebra 3 (1966), 1–27.CrossRefGoogle Scholar
(5)Marcus, M. & Minc, H. Permanents.Amer. Math. Monthly 72 (1965), 577–591.CrossRefGoogle Scholar
(6)Marcus, M. & Minc, H.A survey of matrix theory and matrix inequalities (Allyn and Bacon; Boston, 1964).Google Scholar
(7)Marcus, M., Minc, H. & Newman, M.Inequalities for the permanent function. Ann. of Math. 75 (1962), 47–62.CrossRefGoogle Scholar