No CrossRef data available.
Periodic groups generated by finite amalgams
Published online by Cambridge University Press: 24 October 2008
Extract
The following embedding theorem was proved in the paper (7). Let Π be a set of primes and P, H and K periodic Π-groups satisfying
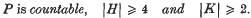
Then there is a period Π-group J generated by isomorphic copies of H and K such that P ≤ J.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 87 , Issue 2 , March 1980 , pp. 189 - 197
- Copyright
- Copyright © Cambridge Philosophical Society 1980
References
REFERENCES
(1)Adyan, S. I.On the simplicity of periodic products of groups. Dokl. Akad. Nauk USSR, 241 (1978) ( = Soviet Math. Dokl. 19 (1978), 910–913).Google Scholar
(2)Adyan, S. I.The Burnside problem and identities in groups (New York, Springer-Verlag, 1978).Google Scholar
(4)Hall, P.On the embedding of a group in a join of given groups. J. Austral. Math. Soc. 17 (1974), 434–495.Google Scholar
(5)Hickin, K. K.An embedding theorem for periodic groups. J. London Math. Soc. (2) 14 (1976), 63–64.CrossRefGoogle Scholar
(6)Hickin, K. K. and Phillips, R. E.Non-isomorphic Burnside groups of exponent p 2. Canad. J. Math. 30 (1978), 180–189.Google Scholar
(7)Hickin, K. K. and Phillips, R. E.Joins of periodic groups. Proc. London Math. Soc. (3) 39 (1979), 176–192.CrossRefGoogle Scholar
(8)Jeanes, S. Counting the periodic subgroups generated by two finite groups. (To appear.)Google Scholar
(9)Karass, A. and Solitar, D.The subgroups of a free product of two groups with an amalgamated subgroup. Trans. Amer. Math. Soc. 150 (1970), 227–255.Google Scholar
(10)Mostowski, A. and Tarski, A.Boolesche Ringe mit geordneter Basis. Fund. Math. 32 (1939), 69–86.Google Scholar
(11)Novikov, P. S. and Adyan, S. I.Infinite periodic groups, Izv. Akad. Nauk USSR Ser. Mat. 32 (1968), 212–244; 251–524; 709–731 (= Math. USSR Izv. 2 (1968), 209–236, 241–479, 665–685).Google Scholar
(12)Phillips, R. E.Embedding methods for periodic groups. Proc. London Math. Soc. (3) 35 (1977), 238–256.Google Scholar
(13)Plotkin, B.I Generalized solvable and generalized nilpotent groups Uspehi. Mat. Nauk (N.S.) 13 (1958), 89–172 ( = Amer. Math. Soc. Transl. (2) 17, 29–116).Google Scholar


