Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T15:17:02.466Z Has data issue: false hasContentIssue false
  • English
  • Français

A partition of non-synthesis for a quotient algebra of A(Z)

Published online by Cambridge University Press:  24 October 2008

D. L. Salinger
D. L. Salinger
Affiliation:
Trinity College, University of Cambridge, and Faculte des Sciences, Orsay
Get access Rights & Permissions [Opens in a new window]

Extract

Let A(Z) be the Banach algebra of Fourier-Lebesgue coefficients: a function f is an element of A(Z) if it is the Fourier transform

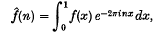
of some function fεL1(T), where T, as usual, denotes the circle group. We write

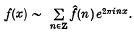
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 68 , Issue 3 , November 1970 , pp. 675 - 683
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Drury, S. W.A partition of non-synthesis in tensor algebras. Proc. Cambridge Philos. Soc. 67 (1970), 19–21.CrossRefGoogle Scholar
(2)Kahane, J. P. Idempotents and closed subalgebras of A(Z). Symposium on Function Algebras. Tulane University (1965).Google Scholar
(3)Kahane, J. P.Algebres tensorielles et analyse harmonique. Siminaire Bourbaki (05 1965).Google Scholar
(4)Katznelson, Y.An introduction to harmonic analysis (Wiley, 1968).Google Scholar
(5)Rudin, W.Fourier analysis on groups (Interscience).Google Scholar
(6)Varopoulos, N. Th.Tensor algebras and harmonic analysis. Acta Math. 119 (1967), 51–112.CrossRefGoogle Scholar
(7)Varopoulos, N. Th.Tensor algebras over discrete spaces. J. Functional Analysis 3 (1969), 321–335.CrossRefGoogle Scholar