The order-bound topology on Riesz spaces
Published online by Cambridge University Press: 24 October 2008
Extract
1. Introduction. Let (X, C) be a Riesz space (or vector lattice) with positive cone C. A subset B of X is said to be solid if it follows from |x| ≤ |b| with b in B that x is in B (where |x| denotes the supremum of x and − x). The solid hull of B (absolute envelope of B in the terminology of Roberts (2)) is denoted to be the smallest solid set containing B, and is denoted by SB. A locally convex Hausdorff topology 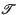 on (X, C) is called a locally solid topology if
on (X, C) is called a locally solid topology if 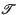 admits a neighbourhood-base of 0 consisting of solid and convex sets in X; and (X, C,
admits a neighbourhood-base of 0 consisting of solid and convex sets in X; and (X, C, 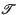 ), where
), where 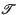 is a locally solid topology, is called a locally convex Riesz space.
is a locally solid topology, is called a locally convex Riesz space.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 67 , Issue 3 , May 1970 , pp. 587 - 593
- Copyright
- Copyright © Cambridge Philosophical Society 1970
References
REFERENCES
- 3
- Cited by


