No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
A three-phase star-connected alternating-current motor of simplest type, connected to busbars maintained at sinusoidal potentials e1, e2 and e3 with respect to the star-point and connected to a shaft load which exerts a reactive torque f on the rotor, is dynamically specified by the following functions:
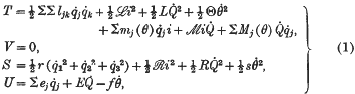
where the 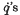 are the armature currents in the three phases, i is the current in the amortisseur circuit, Q the current in the field circuit, θ the rotor position angle, T the kinetic energy, V the potential energy, S the Rayleigh dissipation and U the activity of the external forces on the machine. The self-inductances of the armature circuits and the mutual inductances between them are assumed to be constant.
are the armature currents in the three phases, i is the current in the amortisseur circuit, Q the current in the field circuit, θ the rotor position angle, T the kinetic energy, V the potential energy, S the Rayleigh dissipation and U the activity of the external forces on the machine. The self-inductances of the armature circuits and the mutual inductances between them are assumed to be constant.
† See Ingram, , Proc. Camb. Phil. Soc. 28 (1932), 106CrossRefGoogle Scholar. The formula on p. 108 holds in form when saturation is taken into account, but then the position of the rotor is not accurately given by ψ.
† By a discussion of the determinant given on p. 616 of the Electrician for May 12th, 1933. Routh's criterion has been given a convenient determinantal form by Frazer, and Duncan, , Proc. Roy. Soc. A, 124 (1929), 642.CrossRefGoogle Scholar
‡ Taken from Miles Walker: Specification and Design of Dynamo-Electric Machines, p. 404. For this machine, the following values are taken or computed: r = 0·0004 ohm, l 11 = 3·4 × 10−4, l 12 = − 1·5 × 10−4, l* = 5·0 × 10−4, M 0 = 0·015 and M 0 = 1·0 × 10−4 henrys.
† Cf. Nickle, and Pierce, , Trans. Am. Inst. El. Engrs. 49 (1930), p. 34.Google Scholar
‡ Cf. Moulton, , Periodic Orbits, p. 23.Google Scholar