On the product of three homogeneous linear forms
Published online by Cambridge University Press: 24 October 2008
Extract
Let X denote the general point with coordinates (x1, x2, x3) in 3-dimensional space; and let P(X) be the function defined by
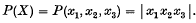
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 47 , Issue 2 , April 1951 , pp. 251 - 259
- Copyright
- Copyright © Cambridge Philosophical Society 1951
References
* Davenport, H.Proc. London Math. Soc. (2), 44 (1938), 412–31CrossRefGoogle Scholar; for a simpler proof, see Davenport, H.J. London Math. Soc. 16 (1941), 98–101.CrossRefGoogle Scholar
† Davenport, H.Proc. Cambridge Phil. Soc. 39 (1943), 1–21.CrossRefGoogle Scholar
‡ Mahler, K.Proc. K. Ned. Akad. Wet. Amsterdam, 49 (1946), 331–43, 444–54, 524–32, 622–31Google Scholar (Theorem M, p. 527).
§ Davenport, H. and Rogers, C. A.Philos. Trans. Roy. Soc. A, 242 (1950), 311–44CrossRefGoogle Scholar, § 8.
∥ Loc. cit., Corollary to Theorem 12.
* J. London Math. Soc. 16 (1941), 98–101.Google Scholar
* Loc. cit. (1941).
* We use the method of Davenport, loc. cit. (1941).
- 2
- Cited by


