Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Samal, G.
and
Mishra, M. N.
1972.
On the lower bound of the number of real roots of a random algebraic equation with infinite variance.
Proceedings of the American Mathematical Society,
Vol. 33,
Issue. 2,
p.
523.
Mishra, M. N.
Nayak, N. N.
and
Pattanayak, S.
1983.
Lower bound for the number of real roots of a random algebraic polynomial.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 35,
Issue. 1,
p.
18.
BHARUCHA-REID, A.T.
and
SAMBANDHAM, M.
1986.
Random Polynomials.
p.
49.
Pratihari, D.
Panda, R. K.
and
Pattanaik, B. P.
1993.
On the number of real roots of a random algebraic equation.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 54,
Issue. 1,
p.
86.
Farahmand, K.
1997.
On the Number of Real Solutions of a Random Polynomial.
Journal of Mathematical Analysis and Applications,
Vol. 213,
Issue. 1,
p.
229.
Uno, Takashi
2007.
On the Lower Bound for the Number of Real Roots of a
Random Algebraic Equation.
Journal of Applied Mathematics and Stochastic Analysis,
Vol. 2007,
Issue. ,
p.
1.


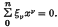 The coefficients ξ
The coefficients ξ