On the motion of a Gaussian wave-packet in a parabolic potential field
Published online by Cambridge University Press: 24 October 2008
Extract
The paper deals with the motion of a Gaussian wave-packet in a parabolic potential field, contrasting the quantum-mechanical behaviour of the packet with that which follows from pure classical mechanics.
The behaviour is entirely classical only if the initial phase of the space-wave-function is linear in the space coordinate; in which case the wave-packet is initially a ‘best-possible’ packet according to Heisenberg's uncertainty relationship.
The paper concludes with a brief reference to the similar problem for a free particle.
Note added in Proof, 16 February 1946. Through the courtesy of Mr M. S. Bartlett, we have been privileged to see the manuscripts of some work by Mr J. E. Moyal and himself, in which the motion of a probability wave-packet is discussed in more general terms than our own: and in which it appears that the motion of our wave-packet, which we have described as non-classical, is indeed actually classical provided that a certain correlation exists between momentum and position in the p, q-distribution function. With this knowledge we now find that classical and quantal predictions agree precisely provided that the initial classical probability function is given by
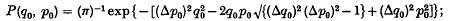
this is a particular case of their more general results.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 42 , Issue 3 , October 1946 , pp. 286 - 291
- Copyright
- Copyright © Cambridge Philosophical Society 1946
References
REFERENCES
- 2
- Cited by


