Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T14:31:35.090Z Has data issue: false hasContentIssue false
  • English
  • Français

On the motion of a flat plate at high speed in a viscous compressible fluid. I. Impulsive motion

Published online by Cambridge University Press:  24 October 2008

K. Stewartson
K. Stewartson
Affiliation:
Guggenheim Aeronautical LaboratoryCalifornia Institute of Technology†
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of giving an infinite plate, immersed in a compressible fluid, an impulsive velocity U in its own plane is examined on the assumption that M = U/a0 ≫ 1 where a0 is the velocity of sound in the undisturbed fluid. To begin with the flow field is very complex but very soon after the motion has begun a shock wave moves at right angles to the plate gradually weakening and eventually degenerating into a sound wave. Attention is concentrated on the flow field when there is a distinct strong shock wave, it being assumed, and justified a posteriori, that the flow behind it may be divided into an inviscid region and a boundary layer region. The equation of the shock wave and a complete description of the flow behind it is found when log M, where ν0 is the coefficient of kinematic viscosity of the undisturbed air. An approximate method is also given to enable the solution to be joined up to Van Dyke's (10) which is valid when .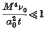

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 51 , Issue 1 , January 1955 , pp. 202 - 219
Copyright
Copyright © Cambridge Philosophical Society 1955

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Eggers, A. J. Jr,. and Syvertson, C. A. NACA TN 2646. March 1952 (unpublished).Google Scholar
(2)Elliot, D. and Probstein, R. (Unpublished.)Google Scholar
(3)Howarth, L.Quart. J. Mech. 4 (1951), 157.CrossRefGoogle Scholar
(4)Illingworth, C. R.Proc. Camb. phil. Soc. 46 (1950), 603.Google Scholar
(5)Kaplun, S.Z. angew. Math. Phys. 5 (1954), 111.CrossRefGoogle Scholar
(6)Lees, L. and Probstein, R. Princeton Univ. Aero. Eng. Lab. Report no. 195 (1952) (unpublished).Google Scholar
(7)Lees, L. and Phobstein, R. Hypersonic flows of a viscous fluid (unpublished).Google Scholar
(8)Li, Ting-Yi and Nagamatsa, H. T.J. Aero. Sci. 20 (1953), 345.Google Scholar
(9)Stewartson, K.J. Aero. Sci. (to be published.)Google Scholar
(10)Van Dyke, M. D.Z. angew. Math. Phys. 3 (1952), 343.CrossRefGoogle Scholar