Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T01:38:51.702Z Has data issue: false hasContentIssue false
  • English
  • Français

On the digits of the multiples of an irrational p-adic number

Published online by Cambridge University Press:  24 October 2008

Kurt Mahler
Kurt Mahler
Affiliation:
Canberra
Get access Rights & Permissions [Opens in a new window]

Extract

Let α be an irrational p-adic number, r an arbitrary positive integer. Our aim is to prove that there exists a rational integer X satisfying

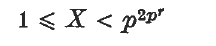
such that every possible sequence of r digits 0, 1, …, p – 1 occurs infinitely often in the canonical p-adic series for Xα. It is clear that it suffices to prove this result for p-adic integers.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 76 , Issue 2 , September 1974 , pp. 417 - 422
Copyright
Copyright © Cambridge Philosophical Society 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)