Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T04:43:17.007Z Has data issue: false hasContentIssue false
  • English
  • Français

On the centres of hereditary JBW-subalgebras of a JBW-algebra

Published online by Cambridge University Press:  24 October 2008

C. M. Edwards
C. M. Edwards
Affiliation:
Department of Mathematics and Statistics, Queen's University, Kingston, Ontario
Get access Rights & Permissions [Opens in a new window]

Extract

A JB-algebra A is a real Jordan algebra, which is also a Banach space, the norm in which satisfies the conditions that

and

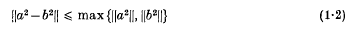
for all elements a and b in A. It follows from (1.1) and (l.2) that

for all elements a and b in A. When the JB-algebra A possesses an identity element then A is said to be a unital JB-algebra and (1.2) is equivalent to the condition that

for all elements a and b in A. For the general theory of JB-algebras the reader is referred to (2), (3), (7) and (10).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 85 , Issue 2 , March 1979 , pp. 317 - 324
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Alfsen, E. M. and Shultz, F. W.Non-commutative spectral theory for affine function spaces on convex sets. Mem. Amer. Math. Soc. 172 (1976), 1–120.Google Scholar
(2)Alfsen, E. M. and Shultz, F. W.State spaces of Jordan algebras. Acta Math. 140 (1978),155–190.CrossRefGoogle Scholar
(3)Alfsen, E. M., Shultz, F. W. and Størmer, E.A Gelfand-Naimark theorem for Jordan algebras. Advances in Math. 28 (1978), 11–57.CrossRefGoogle Scholar
(4)Edwards, C. M.The facial Q-topology for compact convex sets. Math. Arm. 230 (1977), 123–152.Google Scholar
(5)Edwards, C. M., Ideal theory in JB-algebras. J. London Math. Soc. 16 (1977), 507–513.CrossRefGoogle Scholar
(6)Edwards, C. M., On the facial structure of a JB-algebra. J. London Math. Soc. (To appear.)Google Scholar
(7)Jacobson, N.Structure and representations of Jordan algebras. Amer. Math. Soc. Colloq. Publ. 39 (Amer. Math. Soc, Providence 1968). II-2Google Scholar
(8)Sakai, S. C*.algebras and W*.algebras. Ergebnisse der Mathematik 60 (Springer, Berlin, Heidelberg, New York, 1971).Google Scholar
(9)Shultz, F. W.On normed Jordan algebras which are Banach dual spaces. J. Funct. Anal. (To appear.)Google Scholar
(10)Smith, R. R.On non-unital Jordan Banach algebras. Proc. Cambridge Philos. Soc. 82 (1977), 375–380.CrossRefGoogle Scholar
(11)Topping, D. M.Jordan algebras of self-adjoint operators. Mem. Amer. Math. Soc. 53 (1965), 1–48.Google Scholar
(12)Wright, J. D. M.Jordan C*-algebras. Michigan Math. J. (To appear.)Google Scholar