Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Baltes, H.P.
1976.
Planck's radiation law for finite cavities and related problems.
Infrared Physics,
Vol. 16,
Issue. 1-2,
p.
1.
BALTES, H.P.
1976.
International Conference on Infrared Physics (CIRP).
p.
1.
Dowker, J S
and
Kennedy, G
1978.
Finite temperature and boundary effects in static space-times.
Journal of Physics A: Mathematical and General,
Vol. 11,
Issue. 5,
p.
895.
Osserman, Robert
1978.
The isoperimetric inequality.
Bulletin of the American Mathematical Society,
Vol. 84,
Issue. 6,
p.
1182.
Kennedy, G
1978.
Boundary terms in the Schwinger-DeWitt expansion: flat space results.
Journal of Physics A: Mathematical and General,
Vol. 11,
Issue. 8,
p.
L173.
Chen, Bang-Yen
and
Vanhecke, Lieven
1979.
Total curvatures of geodesic spheres.
Archiv der Mathematik,
Vol. 32,
Issue. 1,
p.
404.
Deutsch, D.
and
Candelas, P.
1979.
Boundary effects in quantum field theory.
Physical Review D,
Vol. 20,
Issue. 12,
p.
3063.
Birman, M. Sh.
and
Solomyak, M. Z.
1979.
Asymptotic behavior of the spectrum of differential equations.
Journal of Soviet Mathematics,
Vol. 12,
Issue. 3,
p.
247.
Dikmen, M.
1980.
Thin Shell Theory.
p.
89.
Sen, Siddhartha
1981.
A calculation of the Casimir force on a circular boundary.
Journal of Mathematical Physics,
Vol. 22,
Issue. 12,
p.
2968.
Zayed, Elsayed M.E.
1984.
Differential Equations, Proceedings of the Conference held at The University of Alabama in Birmingham.
Vol. 92,
Issue. ,
p.
599.
Gottlieb, H. P. W.
1985.
Eigenvalues of the Laplacian with Neumann boundary conditions.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 26,
Issue. 3,
p.
293.
Schleich, Kristin
1985.
Semiclassical wave function of the Universe at small three-geometries.
Physical Review D,
Vol. 32,
Issue. 8,
p.
1889.
Gottlieb, H. P. W.
1988.
Eigenvalues of the Laplacian for rectilinear regions.
The Journal of the Australian Mathematical Society. Series B. Applied Mathematics,
Vol. 29,
Issue. 3,
p.
270.
Louko, Jorma
1988.
Quantum cosmology with electromagnetism.
Physical Review D,
Vol. 38,
Issue. 2,
p.
478.
Taubmann, G
1990.
On the shape dependence of the translational partition function.
Journal of Physics A: Mathematical and General,
Vol. 23,
Issue. 19,
p.
4313.
Zayed, E. M. E.
1990.
Hearing the shape of a general doubly connected domain in R3 with impedance boundary conditions.
Journal of Mathematical Physics,
Vol. 31,
Issue. 10,
p.
2361.
McAvity, D M
and
Osborn, H
1991.
A DeWitt expansion of the heat kernel for manifolds with a boundary.
Classical and Quantum Gravity,
Vol. 8,
Issue. 4,
p.
603.
Zayed, E. M. E.
1991.
Hearing the shape of a general doubly-connected domain inR 3 with mixed boundary conditions.
ZAMP Zeitschrift f�r angewandte Mathematik und Physik,
Vol. 42,
Issue. 4,
p.
547.
Zayed, E.M.E.
1991.
Heat equation for a general convex domain inR3with a finite number of piecewise impedance boundary conditions.
Applicable Analysis,
Vol. 42,
Issue. 1-4,
p.
209.

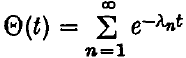 may be constructed in identical fashion; thus
may be constructed in identical fashion; thus