Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Defant, Andreas
and
Maestre, Manuel
1994.
Property (BB) and holomorphic functions on Fréchet-Montel spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 2,
p.
305.
Paúl, Pedro J.
Sáez, Carmen
and
Virués, Juan M.
2000.
Locally Convex Spaces with Toeplitz Decompositions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 68,
Issue. 1,
p.
19.
Defant, Andreas
Díaz, Juan Carlos
García, Domingo
and
Maestre, Manuel
2002.
Existence of Unconditional Bases in Spaces of Polynomials and Holomorphic Functions.
Mathematische Nachrichten,
Vol. 233-234,
Issue. 1,
p.
89.
Albanese, Angela A.
and
Mangino, Elisabetta M.
2011.
Some permanence results of the Dunford-Pettis and Grothendieck properties in lcHs.
Functiones et Approximatio Commentarii Mathematici,
Vol. 44,
Issue. 2,


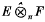 is Montel (resp. distinguished). We also give examples of Montel decomposable (
is Montel (resp. distinguished). We also give examples of Montel decomposable (