Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T02:07:07.799Z Has data issue: false hasContentIssue false
  • English
  • Français

On convex sets and measures

Published online by Cambridge University Press:  24 October 2008

D. G. Larman  and
D. J. Ward
D. G. Larman
Affiliation:
University College London and the University of Sussex
D. J. Ward
Affiliation:
University College London and the University of Sussex
Get access Rights & Permissions [Opens in a new window]

Extract

If α is a positive real number then, for each set E in R3, we define

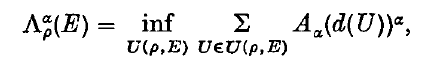
where U(ρ, E) is any countable collection of convex sets, each of diameter at most ρ, whose union covers E, and Aα is a positive real number. Then the convex α-dimensional measure Λα(E), of E, is 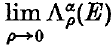. In this paper we shall only be considering the cases α = 1,2 where, as is usual, we take A1 = 1 and A2 = ¼π. The symbols 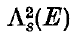,Λs(E) will denote the spherical (circular) measure of E, i.e. when the coverings are restricted to being collections of spheres (circles), and E(z) is the intersection of a set E (in R3) with the plane (x, y) at z.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 1 , January 1966 , pp. 33 - 42
Copyright
Copyright © Cambridge Philosophical Society 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Besicovitch, A. S.Parametric surfaces. II. Proc. Cambridge Philos. Soc. 45 (1949), 14–23.CrossRefGoogle Scholar
(2)Besicovitch, A. S.On surfaces of minimum area. Proc. Cambridge Philos. Soc. 44 (1948), 313–334.CrossRefGoogle Scholar
(3)Ward, D. J.A counter-example in area theory. Proc. Cambridge Philos. Soc. 60 (1964), 821–845.CrossRefGoogle Scholar