Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T01:18:41.561Z Has data issue: false hasContentIssue false
  • English
  • Français

On complete subgraphs of different orders

Published online by Cambridge University Press:  24 October 2008

Béla Bollobás
Béla Bollobás
Affiliation:
Trinity College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

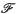Let S be a set and let {X1, …, Xn} = be a family of distinct subsets of S. The intersection graph Ω(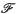) of 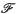has vertex set {X1, …, Xn} and XiXj (i ≠ j) is an edge of Ω(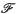) if and only if Xi ∩ Xi ≠ Ø (c.f. (6)). It is easily seen, (7), that every graph is an intersection graph, in other words every graph can be represented by subsets ofa set. Moreover, it was proved by Erdös, Goodman and Pósa (5) that if a graph has n ≥ 4 vertices then one can find a representing set with at most [n2/4] elements. This assertion is an immediate consequence of the result, (5), that the edges of a graph with n ≥ 1 vertices can be covered with at most [n2/4] edge disjoint triangles and edges. We say that a graph G is covered with the subgraphs G1, …, Gk, if every edge of G is in at least one Gi. One of the aims of this note is to prove an extension of this result, pro-posed by Erdös (4).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 79 , Issue 1 , January 1976 , pp. 19 - 24
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bollobás, B.Three-graphs without two triples whose symmetric difference is contained in a third. Discrete Math. 8 (1974), 21–24.CrossRefGoogle Scholar
(2)ErdÖS, P.On a theorem of Rademacher–Turán. Illinois J. Math. 6 (1962), 122–127.CrossRefGoogle Scholar
(3)ErdÖS, P.On the number of complete subgraphs and circuits contained in graphs. Časopis Pěst. Mat. 94 (1969), 290–296.CrossRefGoogle Scholar
(4)ErdÖS, P.Problems and result.s in combinatorial analysis. Technion preprint series No. MT-182, Haifa, 1973.Google Scholar
(5)ErdÖS, P., Goodman, A. and PóSA, L.The representation of graphs by set intersections. Canad. J. Math. 18 (1966), 106–112.CrossRefGoogle Scholar
(6)Harary, F.Graph Theory (Addison-Wesley; Reading, Mass. 1969).CrossRefGoogle Scholar
(7)Marczewski, E.Sur deux propriétés des classes d'ensombles. Fund. Math. 33 (1945), 303–307.CrossRefGoogle Scholar
(8)Moon, J. W. and Moser, L.On a problem of Turán. Magyar Tud. Akad. Mat. KutatóInt. Közl. 7 (1962), 283–286.Google Scholar
(9)Nordhaus, E. A. and Stewabt, B. M.Triangles in an ordinary graph. Caned. J. Math. 15 (1963), 33–41.CrossRefGoogle Scholar
(10)Sauer, N.A generalization of a theorem of Turán (Res. P. No. 61, Dept. Maths., Ca1gary 1968).Google Scholar
(11)Turán, P.On the theory of graphs. Colloq. Math. 3 (1954), 19–30.CrossRefGoogle Scholar