Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
González Díez, Gabino
and
Harvey, William J.
1991.
On complete curves in moduli space II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 110,
Issue. 3,
p.
467.
Zaal, Chris
1995.
Explicit complete curves in the moduli space of curves of genus three.
Geometriae Dedicata,
Vol. 56,
Issue. 2,
p.
185.
Faber, Carel
and
Looijenga, Eduard
1999.
Moduli of Curves and Abelian Varieties.
Vol. 33,
Issue. ,
p.
23.
Bryan, Jim
and
Donagi, Ron
2002.
Surface bundles over surfaces of small genus.
Geometry & Topology,
Vol. 6,
Issue. 1,
p.
59.
Bregman, Corey
2021.
On Kodaira fibrations with invariant cohomology.
Geometry & Topology,
Vol. 25,
Issue. 5,
p.
2385.


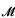
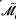
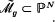 with hypersurfaces in sufficiently general position one obtains a complete curve in
with hypersurfaces in sufficiently general position one obtains a complete curve in 