Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sumners, D.W.
1972.
A note of an example of Poenaru.
Topology,
Vol. 11,
Issue. 3,
p.
319.
Gordon, C. McA.
and
Sumners, D. W.
1975.
Knotted ball pairs whose product with an interval is unknotted.
Mathematische Annalen,
Vol. 217,
Issue. 1,
p.
47.
McCallum, W. A.
1976.
The Higher homotopy groups of the p-spun trefoil knot.
Glasgow Mathematical Journal,
Vol. 17,
Issue. 1,
p.
44.
McCallum, W. A.
1976.
The higher homotopy groups of links.
Journal of Differential Geometry,
Vol. 11,
Issue. 3,
Mielke, Eckehard W.
1977.
Knot wormholes in geometrodynamics?.
General Relativity and Gravitation,
Vol. 8,
Issue. 3,
p.
175.
Swarup, G.Ananda
1977.
Relative version of a theorem of Stallings.
Journal of Pure and Applied Algebra,
Vol. 11,
Issue. 1-3,
p.
75.
Suciu, Alexander I.
1990.
Iterated spinning and homology spheres.
Transactions of the American Mathematical Society,
Vol. 321,
Issue. 1,
p.
145.


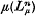 is a smooth embedding of the disjoint union of μ copies of
is a smooth embedding of the disjoint union of μ copies of 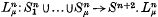 is said to be
is said to be 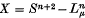 , and
, and 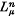 is trivial, then
is trivial, then 