Article contents
Number systems and tilings over Laurent series
Published online by Cambridge University Press: 01 July 2009
Abstract
Let 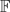 be a field and
be a field and 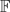 [x, y] the ring of polynomials in two variables over
[x, y] the ring of polynomials in two variables over 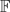 . Let f ∈
. Let f ∈ 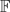 [x, y] and consider the residue class ring R :=
[x, y] and consider the residue class ring R := 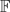 [x, y]/f
[x, y]/f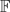 [x, y]. Our first aim is to study digit representations in R, i.e., we ask for which f each element of R admits a digit representation of the form d0 + d1x + ⋅ ⋅ ⋅ + dℓxℓ with digits di ∈
[x, y]. Our first aim is to study digit representations in R, i.e., we ask for which f each element of R admits a digit representation of the form d0 + d1x + ⋅ ⋅ ⋅ + dℓxℓ with digits di ∈ 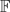 [y] satisfying degy(di) < degy(f). These digit systems are motivated by the well-known notion of canonical number systems. Next we enlarge the ring in order to allow representations including negative powers of the “base” x. In particular, we define and characterize digit representations for the ring S :=
[y] satisfying degy(di) < degy(f). These digit systems are motivated by the well-known notion of canonical number systems. Next we enlarge the ring in order to allow representations including negative powers of the “base” x. In particular, we define and characterize digit representations for the ring S := 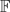 ((x−1, y−1))/f
((x−1, y−1))/f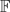 ((x−1, y−1)) and give easy to handle criteria for finiteness and periodicity of such representations. Finally, we attach fundamental domains to our digit systems. The fundamental domain of a digit system is the set of all elements having only negative powers of x in their “x-ary” representation. The translates of the fundamental domain induce a tiling of S. Interestingly, the fundamental domains of our digit systems turn out to be unions of boxes. If we choose
((x−1, y−1)) and give easy to handle criteria for finiteness and periodicity of such representations. Finally, we attach fundamental domains to our digit systems. The fundamental domain of a digit system is the set of all elements having only negative powers of x in their “x-ary” representation. The translates of the fundamental domain induce a tiling of S. Interestingly, the fundamental domains of our digit systems turn out to be unions of boxes. If we choose 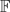 =
=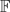 q to be a finite field, these unions become finite.
q to be a finite field, these unions become finite.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 147 , Issue 1 , July 2009 , pp. 9 - 29
- Copyright
- Copyright © Cambridge Philosophical Society 2009
References
REFERENCES
- 7
- Cited by


