Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T12:59:22.189Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the representation of general recursive functions and the μ quantifier

Published online by Cambridge University Press:  24 October 2008

Alan Rose
Alan Rose
Affiliation:
The University Nottingham
Get access Rights & Permissions [Opens in a new window]

Extract

It has been shown that every general recursive function is definable by application of the five schemata for primitive recursive functions together with the schema

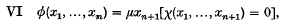
subject to the condition that, for each n–tuple of natural numbers x1,…, xn there exists a natural number xn+1 such that

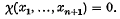
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 55 , Issue 2 , April 1959 , pp. 145 - 148
Copyright
Copyright © Cambridge Philosophical Society 1959

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Kleene, S. C.Introduction to Metamathematics (Amsterdam, 1952).Google Scholar
(2)Łukasiewicz, J. and Tarski, A.Untersuchungen über den Aussagenkalkül. C.R. Acad. Sci., Warsaw (3), 23 (1930), 30–50.Google Scholar
(3)Rose, A.A Gödel Theorem for an infinite-valued Erweiterter Aussagenkalkül. Z. für Math. Logik, 1 (1955), 89–90.Google Scholar
(4)Rosser, J. B. and Turquette, A. R.Many-valued logics (Amsterdam, 1952).Google Scholar
(5)Tarski, A.Logic, semantics, metamathematics (Oxford, 1956).Google Scholar