Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T14:13:49.931Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on desuspending the Adams map

Published online by Cambridge University Press:  24 October 2008

F. R. Cohen  and
J. A. Neisendorfer
F. R. Cohen
Affiliation:
University of Kentuckyand Ohio State University
J. A. Neisendorfer
Affiliation:
University of Kentuckyand Ohio State University
Get access Rights & Permissions [Opens in a new window]

Extract

Let p denote a fixed prime and let Pn(pr) denote the cofibre of the degree pr map on Sn–1. We consider π*P3(pr) and show that the map q in the cofibre sequence

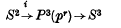
induces a split epimorphism on the p-primary component of π2pS3 if p > 2. That analogous maps q: Pn(pr) →Sn, n ≥ 4, induce split epimorphisms on the p-primary component of πn+2p-3Sn, p > 2, is shown in work of J. F. Adams [1]. It is the purpose of this note to document the above computation in the case n = 3 for the use of others.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 99 , Issue 1 , January 1986 , pp. 59 - 64
Copyright
Copyright © Cambridge Philosophical Society 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adams, J. F.. On the groups J(X), IV. Topology 5 (1966), 21–71.CrossRefGoogle Scholar
[2]Cohen, F. R., Moore, J. C. and Neisendorfer, J. A.. Torsion in homotopy groups. Ann. of Math. 109 (1979), 121–168.CrossRefGoogle Scholar
[3]Cohen, F. R., Moore, J. C. and Neisendorfer, J. A.. The double suspension and p-primary components of the homotopy groups of spheres. Ann. of Math. 110 (1979), 549–565.CrossRefGoogle Scholar
[4]Cohen, F. R., Moore, J. C. and Neisendorfer, J. A.. Exponents in homotopy theory, to appear in the Conference Proceedings in honor of J. C. Moore's 60th birthday.Google Scholar
[5]Neisendorfer, J. A.. Primary homotopy theory. Memoirs of the A.M.S., 232, 1980.Google Scholar
[6]Neisendorfer, J. A.. 3 primary exponents. Math. Proc. Cambridge Philos. Soc. 90 (1981), 163–183.CrossRefGoogle Scholar
[7]Whitehead, G. W.. Elements of Homotopy Theory. Graduate Texts in Mathematics (Springer-Verlag, 1978).CrossRefGoogle Scholar