Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Feng, De-Jun
2012.
Multifractal analysis of Bernoulli convolutions associated with Salem numbers.
Advances in Mathematics,
Vol. 229,
Issue. 5,
p.
3052.
Barral, Julien
and
Feng, De-Jun
2013.
Multifractal Formalism for Almost all Self-Affine Measures.
Communications in Mathematical Physics,
Vol. 318,
Issue. 2,
p.
473.
Kempton, Tom
2014.
On the invariant density of the random β-transformation.
Acta Mathematica Hungarica,
Vol. 142,
Issue. 2,
p.
403.
Neunhäuserer, J.
2015.
Multifractality of overlapping non-uniform self-similar measures.
Monatshefte für Mathematik,
Vol. 177,
Issue. 3,
p.
461.
Allaart, Pieter C.
2017.
Differentiability of a two-parameter family of self-affine functions.
Journal of Mathematical Analysis and Applications,
Vol. 450,
Issue. 2,
p.
954.
Bandt, Christoph
2017.
Recent Developments in Fractals and Related Fields.
p.
39.
Fraser, Jonathan
and
Jordan, Thomas
2017.
The Assouad dimension of self-affine carpets with no grid structure.
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 11,
p.
4905.
Allaart, Pieter C.
2017.
On univoque and strongly univoque sets.
Advances in Mathematics,
Vol. 308,
Issue. ,
p.
575.
Bandt, Christoph
2018.
Finite orbits in multivalued maps and Bernoulli convolutions.
Advances in Mathematics,
Vol. 324,
Issue. ,
p.
437.
BAKER, SIMON
and
KONG, DERONG
2019.
Numbers with simply normal β-expansions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 167,
Issue. 01,
p.
171.
Allaart, Pieter
and
Kong, Derong
2019.
On the continuity of the Hausdorff dimension of the univoque set.
Advances in Mathematics,
Vol. 354,
Issue. ,
p.
106729.
Baker, Simon
2019.
Exceptional digit frequencies and expansions in non-integer bases.
Monatshefte für Mathematik,
Vol. 190,
Issue. 1,
p.
1.
BAKER, SIMON
2020.
Digit frequencies and self-affine sets with non-empty interior.
Ergodic Theory and Dynamical Systems,
Vol. 40,
Issue. 7,
p.
1755.
Ngai, Sze-Man
Tang, Wei
and
Xie, Yuanyuan
2020.
Wave Propagation Speed on Fractals.
Journal of Fourier Analysis and Applications,
Vol. 26,
Issue. 2,
Li, Y.-Q.
2020.
Digit frequencies of beta-expansions.
Acta Mathematica Hungarica,
Vol. 162,
Issue. 2,
p.
403.
ALLAART, PIETER
and
KONG, DERONG
2021.
Relative bifurcation sets and the local dimension of univoque bases.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 8,
p.
2241.
Li, Yao-Qiang
2023.
Bifurcations of digit frequencies in unique expansions.
Journal of Number Theory,
Vol. 248,
Issue. ,
p.
420.
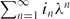 , where in is a sequence of i.i.d. random variables taking the values 0, 1 with probabilities p, 1 − p. These measures are the well-known (biased) Bernoulli convolutions.
, where in is a sequence of i.i.d. random variables taking the values 0, 1 with probabilities p, 1 − p. These measures are the well-known (biased) Bernoulli convolutions.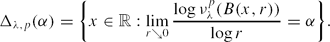 Our main results highlight the fact that for almost all, and in some cases all, λ in an appropriate range, Δλ, p(α) is nonempty and, moreover, has positive Hausdorff dimension, for many values of α. This happens even in parameter regions for which νpλ is typically absolutely continuous.
Our main results highlight the fact that for almost all, and in some cases all, λ in an appropriate range, Δλ, p(α) is nonempty and, moreover, has positive Hausdorff dimension, for many values of α. This happens even in parameter regions for which νpλ is typically absolutely continuous.

