Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T12:40:57.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Morita context functors

Published online by Cambridge University Press:  24 October 2008

W. K. Nicholson  and
J. F. Watters
W. K. Nicholson
Affiliation:
Department of Mathematics and Statistics, University of Calgary, Calgary, Alberta, Canada, T2N 1N4
J. F. Watters
Affiliation:
Department of Mathematics, University of Leicester, Leicester, LEI 7RH
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a Morita context (R, V, W, S), there are functors W⊗() and hom (V, ) from R-mod to; S-mod and a natural transformation λ from the first to the second. This has an epi-mono factorization and the intermediate functor we denote by ()° with natural transformations 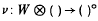and 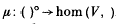. The tensor functor is exact if and only if WR is flat, whilst the hom functor is exact if and only if RV is projective. We begin by determining conditions under which ()° is exact; this is Theorem 1.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 103 , Issue 3 , May 1988 , pp. 399 - 408
Copyright
Copyright © Cambridge Philosophical Society 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Amitsur, S. A.. Rings of quotients and Morita contexts. J. Algebra 17 (1971), 273–298.CrossRefGoogle Scholar
[2]Azumaya, G.. Some properties of TTP-classes. In Proc. Conference on Orders, Group Rings and Related Topics, Lecture Notes in Math. Vol. 353 (Springer-Verlag, 1973), pp. 72–83.CrossRefGoogle Scholar
[3]Chase, S. U.. Direct products of modules. Trans. Amer. Math. Soc. 97 (1960), 457–473.CrossRefGoogle Scholar
[4]Cohn, P. M.. Morita equivalence and duality. Queen Mary College Mathematics Notes, 1966.Google Scholar
[5]Desale, G. and Nicholson, W. K.. Endoprimitive rings. J. Algebra 70 (1980), 548–560.CrossRefGoogle Scholar
[6]Müller, B. J.. The quotient category of a Morita context. J. Algebra 28 (1974), 389–407.CrossRefGoogle Scholar
[7]Nicholson, W. K. and Wattebs, J. F.. Normal classes of prime rings determined by modules. Proc. Amer. Math. Soc. 83 (1981), 27–30.CrossRefGoogle Scholar
[8]Stenström, B.. Rings of Quotients (Springer-Verlag, 1975).CrossRefGoogle Scholar
[9]Zelmanowitz, J. M.. The structure of rings with faithful, non-singular modules. Trans. Amer. Math. Soc. 278 (1983), 347–359.CrossRefGoogle Scholar
[10]Zelmanowitz, J. M.. Representation of rings with faithful monoform modules. J. London Math. Soc. 29 (1984), 237–248.CrossRefGoogle Scholar
[11]Zelmanowitz, J. M.. Representations of rings with faithful polyform modules. Comm. Algebra 14 (1986), 1141–1169.CrossRefGoogle Scholar