Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T02:10:40.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Monotone Lagrangians in 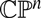${\mathbb{C}}{\mathbb{P}}^n$ of minimal Maslov number n + 1

Part of: Symplectic geometry, contact geometry

Published online by Cambridge University Press:  21 February 2020

MOMCHIL KONSTANTINOV  and
JACK SMITH
MOMCHIL KONSTANTINOV
Affiliation:
Department of Mathematics, University College London, Gower Street, London, WC1E 6BT. e-mail: [email protected]
JACK SMITH
Affiliation:
St John’s College, Cambridge, CB2 1TP. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that a monotone Lagrangian L in 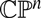${\mathbb{C}}{\mathbb{P}}^n$ of minimal Maslov number n + 1 is homeomorphic to a double quotient of a sphere, and thus homotopy equivalent to 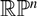${\mathbb{R}}{\mathbb{P}}^n$. To prove this we use Zapolsky’s canonical pearl complex for L over 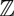${\mathbb{Z}}$, and twisted versions thereof, where the twisting is determined by connected covers of L. The main tool is the action of the quantum cohomology of 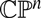${\mathbb{C}}{\mathbb{P}}^n$ on the resulting Floer homologies.

MSC classification

Primary: 53D12: Lagrangian submanifolds; Maslov index
Secondary: 53D40: Floer homology and cohomology, symplectic aspects
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 1 , July 2021 , pp. 1 - 21
Copyright
© Cambridge Philosophical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abouzaid, M.. Nearby Lagrangians with vanishing Maslov class are homotopy equivalent. Invent. Math. 189 (2012), 251–313.CrossRefGoogle Scholar
Albers, P.. A Lagrangian Piunikhin–Salamon–Schwarz morphism and two comparison homomorphisms in Floer homology. Int. Math. Res. Not. IMRN (2008).Google Scholar
Auroux, D.. Mirror symmetry and T-duality in the complement of an anticanonical divisor. J. Gökova Geom. Topol. GGT 1 (2007), 51–91.Google Scholar
Banyaga, A., Hurtubise, D. and Spaeth, P.. Twisted Morse complexes. arXiv:1911.07818.Google Scholar
Biran, P.. Lagrangian non-intersections. Geom. Funct. Anal. 16 (2006), 279–326.10.1007/s00039-006-0560-0CrossRefGoogle Scholar
Biran, P. and Cieliebak, K.. Symplectic topology on subcritical manifolds. Comment. Math. Helv. 76 (2001), 712–753.CrossRefGoogle Scholar
Biran, P. and Cornea, O.. Quantum structures for Lagrangian submanifolds. arXiv:0708.4221v1.Google Scholar
Biran, P. and Cornea, O.. Rigidity and uniruling for Lagrangian submanifolds. Geom. Topol. 13 (2009), 2881–2989.10.2140/gt.2009.13.2881CrossRefGoogle Scholar
Borman, M. S., Li, T.J. and Wu, W.. Spherical Lagrangians via ball packings and symplectic cutting. Selecta Math. (N.S.) 20 (2014), 261–283.CrossRefGoogle Scholar
Campana, F.. On twistor spaces of the class $\mathscr C$ . J. Differential Geom. 33 (1991), 541–549.10.4310/jdg/1214446329CrossRefGoogle Scholar
Cappell, S. E. and Shaneson, J. L.. Some new four-manifolds. Ann. of Math. (2) 104 (1976), 61–72.CrossRefGoogle Scholar
Damian, M.. Floer homology on the universal cover, Audin’s conjecture and other constraints on Lagrangian submanifolds. Comment. Math. Helv. 87 (2012), 433–462.CrossRefGoogle Scholar
Fukaya, K., Seidel, P. and Smith, I.. Exact Lagrangian submanifolds in simply-connected cotangent bundles. Invent. Math. 172 (2008), 1–27.10.1007/s00222-007-0092-8CrossRefGoogle Scholar
Hirsch, M. W. and Milnor, J.. Some curious involutions of spheres. Bull. Amer. Math. Soc. 70 (1964), 372–377.10.1090/S0002-9904-1964-11103-4CrossRefGoogle Scholar
Kollár, J., Miyaoka, Y. and Mori, S.. Rational connectedness and boundedness of Fano manifolds. J. Differential Geom. 36 (1992), 765–779.10.4310/jdg/1214453188CrossRefGoogle Scholar
Konstantinov, M.. Symplectic topology of projective space: Lagrangians, local systems and twistors. Ph.D. thesis, University College London (2019).Google Scholar
Kragh, T.. Parametrized ring-spectra and the nearby Lagrangian conjecture. Geom. Topol. 17 (2013), 639–731. With an appendix by Mohammed Abouzaid.10.2140/gt.2013.17.639CrossRefGoogle Scholar
Kragh, T.. Homotopy equivalence of nearby Lagrangians and the Serre spectral sequence. Math. Ann. 368 (2017), 945–970.10.1007/s00208-016-1447-5CrossRefGoogle Scholar
Livesay, G. R.. Fixed-point-free involutions on the 3-sphere. In Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), p. 220 (Prentice-Hall, Englewood Cliffs, N.J. 1962).10.2307/1970232CrossRefGoogle Scholar
May, J. P.. The dual Whitehead theorems. In Topological topics, volume 86 of London Math. Soc. Lecture Note Ser., 46–54 (Cambridge University Press, Cambridge 1983).Google Scholar
McDuff, D. and Salamon, D.. J-holomorphic curves and quantum cohomology, volume 6 of University Lecture Series (American Mathematical Society, Providence, RI 1994).Google Scholar
Nadler, D.. Microlocal branes are constructible sheaves. Selecta Math. (N.S.) 15 (2009), 563–619.CrossRefGoogle Scholar
Oh, Y.-G.. Floer cohomology, spectral sequences, and the Maslov class of Lagrangian embeddings. Internat. Math. Res. Notices (1996), 305–346.CrossRefGoogle Scholar
Piunikhin, S., Salamon, D. and Schwarz, M.. Symplectic Floer–Donaldson theory and quantum cohomology. In Contact and symplectic geometry (Cambridge, 1994), volume 8 of Publ. Newton Inst., 171–200 (Cambridge University Press, Cambridge 1996).Google Scholar
Schatz, S.. Sur la topologie des sous-variétés Lagrangiennes monotones de l’espace projectif complexe. Ph.D. thesis, Strasbourg (2016).Google Scholar
Seidel, P.. Graded Lagrangian submanifolds. Bull. Soc. Math. France 128 (2000), 103–149.CrossRefGoogle Scholar
Seidel, P.. Fukaya categories and Picard–Lefschetz theory. Zurich Lectures in Advanced Mathematics (European Mathematical Society (EMS), Zürich 2008).CrossRefGoogle Scholar
Sheridan, N.. On the Fukaya category of a Fano hypersurface in projective space. Publ. Math. Inst. Hautes Études Sci. 124 (2016), 165–317.10.1007/s10240-016-0082-8CrossRefGoogle Scholar
Smith, J.. Symmetry in monotone Lagrangian Floer theory. Ph.D. thesis, University of Cambridge (2017).Google Scholar
Zapolsky, F.. The Lagrangian Floer-quantum-PSS package and canonical orientations in Floer theory. arXiv:1507.02253v2.Google Scholar
Zinger, A.. The determinant line bundle for Fredholm operators: construction, properties and classification. Math. Scand. 118 (2016), 203–268.CrossRefGoogle Scholar