Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-24T17:29:09.466Z Has data issue: false hasContentIssue false
  • English
  • Français

Modifications of Fourier transforms and singular continuous measures

Published online by Cambridge University Press:  24 October 2008

Alan MacLean
Alan MacLean
Affiliation:
Wichita State University, Wichita, Kansas, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

It has long been known, after Wiener (e.g. see (11), vol. 1, p. 108, (5), (8), §5·6)) that a measure μ whose Fourier transform 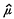vanishes at infinity is continuous, and generally, that μ is continuous if and only if 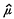is small ‘on the average’. Baker (1) has pursued this theme and obtained concise necessary and sufficient conditions for the continuity of μ, again expressed in terms of the rate of decrease of 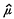. On the other hand, for continuous μ, Rudin (9) points out the difficulty in obtaining criteria based solely on the asymptotic behaviour of 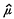by which one may determine whether μ has a singular component. The object of this paper is to show further that any such criteria must be complicated indeed. We shall show that the absolutely continuous measures on T = [0, 2π) whose Fourier transforms are the most well-behaved (namely, those of the form (1/2π)f(x)dx, where f has an absolutely convergent Fourier series) are such that one may modify their transforms on ‘large’ subsets of Z so that they become the transforms of singular continuous measures. Moreover, the singular continuous measures in question may be chosen so that their Fourier transforms do not vanish at infinity.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 87 , Issue 3 , May 1980 , pp. 383 - 392
Copyright
Copyright © Cambridge Philosophical Society 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Baker, R. C.On Wiener's theorem on Fourier–Stieltjes coefficients and the Gaussian law. Proc. London Math. Soc. (3) 25 (1972), 525–542.CrossRefGoogle Scholar
(2)Brown, G.Riesz products and generalized characters. Proc. London Math. Soc. (3) 30 (1975), 209–238.CrossRefGoogle Scholar
(3)Brown, G. and Hewitt, E. Continuous singular measures with small Fourier–Stieltjes transforms. (To appear.)Google Scholar
(4)Brown, G. and Moran, W.On orthogonality of Riesz products. Proc. Cambridge Philos. Soc. 76 (1974), 173–181.CrossRefGoogle Scholar
(5)Hewitt, E. and Stromberg, K.A remark on Fourier–Stieltjes transforms. An. Acad. Brasil Ci. 34 (1962), 175–180.Google Scholar
(6)Hewitt, E. and Zuckerman, H. S.Singular measures with absolutely continuous convol-ution squares. Proc. Cambridge Philos. Soc. 62 (1966), 399–420.CrossRefGoogle Scholar
Corrigendum, Proc. Cambridge Philos. Soc. 63 (1967), 367–368.Google Scholar
(7)MacLean, A.Products of singular continuous measures. Proc. Amer. Math. Soc. 68 (1978), 85–89.CrossRefGoogle Scholar
(8)Rudin, W.Fourier Analysis on Groups (New York, Interscience, 1962).Google Scholar
(9)Rudin, W.Modification of Fourier transforms. Proc. Amer. Math. Soc. 19 (1968), 1069–1074.CrossRefGoogle Scholar
(10)Zygmund, A.On lacunary trigonometric series. Trans. Amer. Math. Soc. 34 (1932), 435–446.CrossRefGoogle Scholar
(11)Zygmund, A.Trigonometric Series, 2nd ed., vol. i, ii (Cambridge University Press, 1959).Google Scholar