Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T13:14:08.709Z Has data issue: false hasContentIssue false
  • English
  • Français

The minimal extension of P-localization on groups

Published online by Cambridge University Press:  24 October 2008

A. J. Berrick  and
G. C. Tan
A. J. Berrick
Affiliation:
Department of Mathematics, Faculty of Science, National University of Singapore, Kent Ridge Crescent, Singapore0511
G. C. Tan
Affiliation:
Department of Mathematics, Faculty of Science, National University of Singapore, Kent Ridge Crescent, Singapore0511
Get access Rights & Permissions [Opens in a new window]

Extract

Let P be a fixed set of primes, the category of all groups and group-homomorphisms, and 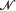the full subcategory of nilpotent groups. In [9], an idempotent functor called P-localization, was defined so as to extend the ℤ-module-theoretic localization of abelian groups. There are two well-known extensions of e to , namely, Bousfield's P-localization [2], [4], denoted by EZP, and Ribenboim's P-localization [13], usually denoted by ( )P. Ribenboim's P-localization is the maximal extension among localizations extending e to in that it maximizes the number of groups in its image [7]. The localized groups obtained after applying Ribenboim's P-localization are precisely the P-local groups, that is, the groups having unique nth-root for every n whichis co-prime to P, [13]. Being maximal is equivalent to this class of P-localized groups being the saturated class of groups generated by e–equivalences, that is, group homomorphisms between nilpotent groups which become isomorphisms after applying e.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 119 , Issue 2 , February 1996 , pp. 243 - 255
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Berrick, A. J. and Casacuberta, C.. Groups and spaces with all localizations trivial. 1990 Barcelona Conference on Algebraic Topology. Lecture Notes in Math. 1509 (Springer, 1992), pp. 20–29.Google Scholar
[2]Bousfield, A. K.. The localization of spaces with respect to homology. Topology 14 (1975), 133–150.CrossRefGoogle Scholar
[3]Bousfield, A. K.. Constructions of factorization system in categories. J. Pure Appl. Algebra 9 (1977), 207–220.CrossRefGoogle Scholar
[4]Bousfield, A. K.. Homological localization towers for groups and π-modules. Mem. Amer. Math. Soc. 10 (1977), no. 186.Google Scholar
[5]Bousfield, A. K. and Kan, D. M.. Homotopy limits, completions and localizations, Lecture Notes in Math. 304 (Springer-Verlag, 1972).CrossRefGoogle Scholar
[6]Casacuberta, C., Frei, A. and Tan, G. C.. Extending localization functors. J. Pure Appl. Algebra (to appear).Google Scholar
[7]Casacuberta, C., Peschke, G. and Pfenniger, M.. On orthogonal pairs in categories and localisation. In Proc. Adams Memorial Symposium, London Math. Soc. Lecture Note Ser. 175 (Cambridge University Press 1992), pp. 211–223.Google Scholar
[8]Cassidy, C., Hebert, M. and Kelly, G. M.. Reflective subcategories, localizations and factorization systems. J. Austral. Math. Soc. (Series A) 38 (1985), 287–329.CrossRefGoogle Scholar
[9]Hilton, P., Mislin, G. and Roitberg, J.. Localization of nilpotent groups and spaces (North Holland, 1975).Google Scholar
[10]Herrlich, H. and Strecker, G. E.. Category theory (Heldermann, 1979).Google Scholar
[11]Kelly, G. M.. On the ordered set of reflective subcategories. Bull. Austral. Math. Soc. 36 (1987), 137–152.CrossRefGoogle Scholar
[12]MacLane, S.. Categories for the working mathematician (Springer-Verlag, 1972).Google Scholar
[13]Ribenboim, P.. Equations in groups, with special emphasis on localization and torsion (II). Portugal Math. 44 (1987), 417–445.Google Scholar
[14]Robinson, D. J. S.. A course in the theory of groups (Springer-Verlag, 1982).CrossRefGoogle Scholar
[15]Warfield, R. B.. Nilpotent groups. Lecture Notes in Maths. 513 (Springer-Verlag, 1976).CrossRefGoogle Scholar