Published online by Cambridge University Press: 20 November 2009
For P ⊂  3 a finite volume geodesic polyhedron, with the property that all interior angles between incident faces are of the form π/mij (mij ≥ 2 an integer), there is a naturally associated Coxeter group ΓP. Furthermore, this Coxeter group is a lattice inside the semi-simple Lie group O+(3, 1) = Isom(
3 a finite volume geodesic polyhedron, with the property that all interior angles between incident faces are of the form π/mij (mij ≥ 2 an integer), there is a naturally associated Coxeter group ΓP. Furthermore, this Coxeter group is a lattice inside the semi-simple Lie group O+(3, 1) = Isom( 3), with fundamental domain the original polyhedron P. In this paper, we provide a procedure for computing the lower algebraic K-theory of the integral group ring of such groups ΓP in terms of the geometry of the polyhedron P. As an ingredient in the computation, we explicitly calculate the K−1 and Wh of the groups Dn and Dn ×
3), with fundamental domain the original polyhedron P. In this paper, we provide a procedure for computing the lower algebraic K-theory of the integral group ring of such groups ΓP in terms of the geometry of the polyhedron P. As an ingredient in the computation, we explicitly calculate the K−1 and Wh of the groups Dn and Dn × 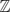 3, and we also summarize what is known about the
3, and we also summarize what is known about the 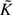 0.
0.