Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Miller, Haynes R.
1981.
On relations between Adams spectral sequences, with an application to the stable homotopy of a moore space.
Journal of Pure and Applied Algebra,
Vol. 20,
Issue. 3,
p.
287.
Harper, J. R.
and
Miller, H. R.
1982.
On the double suspension homomorphism at odd primes.
Transactions of the American Mathematical Society,
Vol. 273,
Issue. 1,
p.
319.
1986.
Vol. 121,
Issue. ,
p.
395.
Davis, Donald M.
and
Mahowald, Mark
1988.
𝑣₁-periodic 𝐸𝑥𝑡 over the Steenrod algebra.
Transactions of the American Mathematical Society,
Vol. 309,
Issue. 2,
p.
503.
Shick, Paul
1988.
Odd primary periodic phenomena in the classical Adams spectral sequence.
Transactions of the American Mathematical Society,
Vol. 309,
Issue. 1,
p.
77.
Thompson, Robert D.
1990.
The 𝑣₁-periodic homotopy groups of an unstable sphere at odd primes.
Transactions of the American Mathematical Society,
Vol. 319,
Issue. 2,
p.
535.
Davis, Donald M.
and
Mahowald, Mark
1990.
v 1-Periodicity in the unstable adams spectral sequence.
Mathematische Zeitschrift,
Vol. 204,
Issue. 1,
p.
319.
Palmieri, John H.
1996.
Nilpotence for modules over the mod2 Steenrod algebra, II.
Duke Mathematical Journal,
Vol. 82,
Issue. 1,
Hess, Kathryn
and
Levi, Ran
2007.
An algebraic model for the loop space homology of a homotopy fiber.
Algebraic & Geometric Topology,
Vol. 7,
Issue. 4,
p.
1699.
Andrews, Michael
and
Miller, Haynes
2017.
Inverting the Hopf map.
Journal of Topology,
Vol. 10,
Issue. 4,
p.
1145.
Belmont, Eva
2020.
Localizing the E2 page of the Adams spectral
sequence.
Algebraic & Geometric Topology,
Vol. 20,
Issue. 4,
p.
1965.
Zhang, Zhilei
Wang, Xiangjun
and
Zhong, Linan
2025.
The Cohomology of P(2) in Dimensions Less Than 4 at an Odd Prime.
Frontiers of Mathematics,


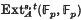 , is zero for
, is zero for 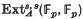 is the one-dimensional vector space generated by
is the one-dimensional vector space generated by 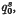 where
where 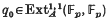 corresponds to the Bockstein.
corresponds to the Bockstein.