Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T10:19:02.081Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear bounds on characteristic polynomials of matroids

Published online by Cambridge University Press:  10 January 2019

SUIJIE WANG ,
YEONG–NAN YEH  and
FENGWEI ZHOU
SUIJIE WANG
Affiliation:
Institute of Mathematics, Hunan University, China. e-mail: [email protected]
YEONG–NAN YEH
Affiliation:
Institute of Mathematics, Academia Sinica, Taiwan. e-mail: [email protected]
FENGWEI ZHOU
Affiliation:
Department of Mathematics, Hong Kong University of Science and Technology, Hong Kong. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let χ(t) = a0tn – a1tn−1 + ⋯ + (−1)rartn−r be the chromatic polynomial of a graph, the characteristic polynomial of a matroid, or the characteristic polynomial of an arrangement of hyperplanes. For any integer k = 0, 1, …, r and real number x ⩾ k − r − 1, we obtain a linear bound of the coefficient sequence, that is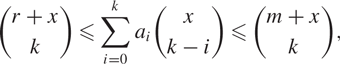

\begin{align*} {r+x\choose k}\leqslant \sum_{i=0}^{k}a_{i}{x\choose k-i}\leqslant {m+x\choose k}, \end{align*}
where m is the size of the graph, matroid, or hyperplane arrangement. It extends Whitney’s sign-alternating theorem, Meredith’s upper bound theorem, and Dowling and Wilson’s lower bound theorem on the coefficient sequence. In the end, we also propose a problem on the combinatorial interpretation of the above inequality.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 168 , Issue 3 , May 2020 , pp. 505 - 518
Copyright
Copyright © Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

This work was supported by the National Natural Science Foundation of China (11871204).

References

REFERENCES

[1]Adiprasto, K.,Huh, J. andKatz, E.. Hodge theory for combinatorial geometries. arXiv:1511.02888.Google Scholar
[2]Chari, M. K.. Two decompositions in topological combinatorics with applications to matroid complexes. Trans. Am. Math. Soc. 349 (1997), 3925–3943.CrossRefGoogle Scholar
[3]D’Adderio, M.,Moci, L. and Arithmetic matroids. The Tutte polynomial and toric arrangement. Adv. Math. 232 (2013), 335–367.CrossRefGoogle Scholar
[4]Dowling, T. A. andWilson, R. M.. The slimmest geometric lattices. Trans. Am. Math. Soc. 196 (1974), 203–215.CrossRefGoogle Scholar
[5]Hibi, T.. Face number inequalities for matroid complexes and Cohen–Macaulay types of Stanley–Reisner rings of distributive lattices. Pac. J. Math. 154 (1992), no. 2, 253–264.CrossRefGoogle Scholar
[6]Lenz, M.. The f-vector of a representable-matroid complex is log-concave. Adv. Appl. Math. 51 (2013), no. 5, 543–545.CrossRefGoogle Scholar
[7]Huh, J.. Milnor numbers of projective hypersurfaces and the chromatic polynomial of graphs. J. Am. Math. Soc. 25 (2012), 907–927.CrossRefGoogle Scholar
[8]Huh, J. andKatz, E.. Log-concavity of characteristic polynomials and Bergman fan of matroids. Math. Ann. 354 (2012), 1103–1116.CrossRefGoogle Scholar
[9]Huh, J.. h-vectors of matroids and logarithmic concavity. Adv. Math. 270 (2015), 49–59.CrossRefGoogle Scholar
[10]Meredith, G. H. J.. Coefficients of chromatic polynomials. J. Combin. Theory Ser. B 13 (1972), 14–17.CrossRefGoogle Scholar
[11]Moci, L.. A Tutte polynomial for toric arrangements. Trans. Am. Math. Soc. 364 (2012) 1067–1088.CrossRefGoogle Scholar
[12]Orlik, P. andTerao, H.. Arrangements of Hyperplanes (Springer–Verlag, Berlin, 1992).CrossRefGoogle Scholar
[13]Oxley, J. G.. Matroid Theory (Oxford University Press, Oxford, 2011).CrossRefGoogle Scholar
[14]Read, R. C.. An introduction to chromatic polynomials. J. Comb. Theory 4 (1968), 52–71. MR0224505(37:104).CrossRefGoogle Scholar
[15]Swartz, E.. Lower bounds for h-vectors of k-CM, independence, and broken circuit complexes. SIAM J. Discrete Math. 18 (2004/05), no. 3, 647–661.CrossRefGoogle Scholar
[16]Stanley, R. P.. An introduction to hyperplane arrangements. In: edited byMiller, E.,Reiner, V.,Sturmfels, B.. Geometric Combinatorics. IAS/Park City Math. Ser., vol. 13. (American Mathematical Society, Providence, RI, 2007), 389–496.CrossRefGoogle Scholar
[17]Wagner, D. G.. Negatively correlated random variables and Mason’s conjecture for independent sets in matroids. Ann. Comb. 12 (2008), no. 2, 211–239.CrossRefGoogle Scholar
[18]White, N.. Theory of Matroids. In: Encyclopedia of Mathematics and its Applications, vol. 26. (Cambridge University Press, Cambridge, 1986).Google Scholar
[19]Whitney, H.. A logical expansion in mathematics. Bull. Am. Math. Soc. 38 (1932), 572–579.CrossRefGoogle Scholar
[20]Whitney, H.. The coloring of graphs. Ann. Math. 33 (1932), no. 2, 688–718.CrossRefGoogle Scholar
[21]Whitney, H.. On the abstract properties of linear dependence. Am. J. Math. 57 (1935) 509–533.CrossRefGoogle Scholar
[22]Wilf, H. S.. Which polynomials are chromatic? Colloquio Internazionale sulle Teorie Combinatorie (1976), 247–256.Google Scholar
[23]Zaslavsky, T.. Facing up to arrangements: Face-count formulas for partitions of space by hyperplanes. Mem. Am. Math. Soc. 1 (1975) no. 154.Google Scholar