Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T12:34:13.558Z Has data issue: false hasContentIssue false
  • English
  • Français

The limits of classical scattering

Published online by Cambridge University Press:  24 October 2008

P. M. S. Blackett
P. M. S. Blackett
Affiliation:
Fellow of King's College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

The methods of geometrical optics provide an approximate solution of the equation of wave propagation, if the following condition, given by De Broglie, is satisfied. If V is the phase velocity, λ the wave-length, l the direction of greatest increase of V, and θ the angle between l and V, then the condition is that

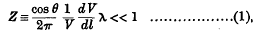
that is, the relative change of V over a distance of the order of θ must be small†.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 23 , Issue 6 , April 1927 , pp. 698 - 702
Copyright
Copyright © Cambridge Philosophical Society 1927

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* De Broglie, , Journ. de Phys. (1926), p. 322.Google Scholar

† In De Broglie's statement of the condition the direction l is left undefined. For a plane wave it can be proved that l most be taken as the direction of greatest increase of V. I am indebted to Mr L. H. Thomas for pointing oat that if the wave is not plane, the condition (l) will contain other terms involving the curvature of the wavefront. It seems unlikely that these terms will be of importance in the cases discussed in this paper.

‡ Wentzel, , Zeit. für Phys., vol. XL (1926), p. 690.Google Scholar

* Schrodinger, , Ann. d. Phys. vol. LXXIX (1926), p. 496.Google Scholar

† It should be noticed that though the cnrvatnre has its greatest value at the apse, the quantity Z has its maximum some distance away from the apse. Since Z contains the factor cos θ it is zero at the apse. There can therefore be no general relation between Schrödinger's and De Broglie's conditions. For instance, for a particle in a circular orbit, Z = 0, whatever the size of the orbit.

‡ Bieler, , Proc. Roy. Soc. A, vol. cv (1924), p. 434.CrossRefGoogle Scholar

* Chadwick, and Bieler, , Phil. Mag., vol. XLII (1921), p. 923.CrossRefGoogle Scholar

† Butherford, and Chadwick, , Phil. Mag., vol. L (1925), p. 889.CrossRefGoogle Scholar

* Elsasser, , Naturwissenschaften, vol. xiii (1925), p. 711.CrossRefGoogle Scholar

† Dymond, , Nature, vol. cxviii (1926), p. 336.CrossRefGoogle Scholar