No CrossRef data available.
Lifting convergent sequences with networks
Published online by Cambridge University Press: 24 October 2008
Extract
Definition (Moukoko Priso(2)). A locally convex spaceE[T] is said to have a strict absorbent network of type Σ if there exists in E a family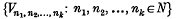 of absolutely convex absorbent sets such that
of absolutely convex absorbent sets such that
(1) if {nk} is a sequence of positive integers and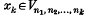 for each k, then the series
for each k, then the series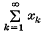 converges in E[T]
converges in E[T]
(2) for each sequence {nk} there is a sequence {λk} of positive real numbers such that, if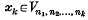 and 0 ≤ μk ≤ λkfor each k, then
and 0 ≤ μk ≤ λkfor each k, then
(i) 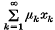 converges in E[T], and
converges in E[T], and
(ii) 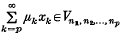 for each p.
for each p.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 70 , Issue 1 , July 1971 , pp. 27 - 30
- Copyright
- Copyright © Cambridge Philosophical Society 1971
References
REFERENCES
(1)Husain, T.The open mapping and closed graph theorems in topological vector spaces (Oxford, 1965)CrossRefGoogle Scholar
(2)Moukoko Priso, P.Sur les questions de relèvement de suites convergentes. C.R. Acad. Sci., Paris, Sér. A 269 (1969), 1063–1065.Google Scholar
(3)de Wilde, M.Réseaux dans les espaces linéaires à semi-normes. Mem. Soc. Roy. Sci. Liège 17 (1969).Google Scholar


